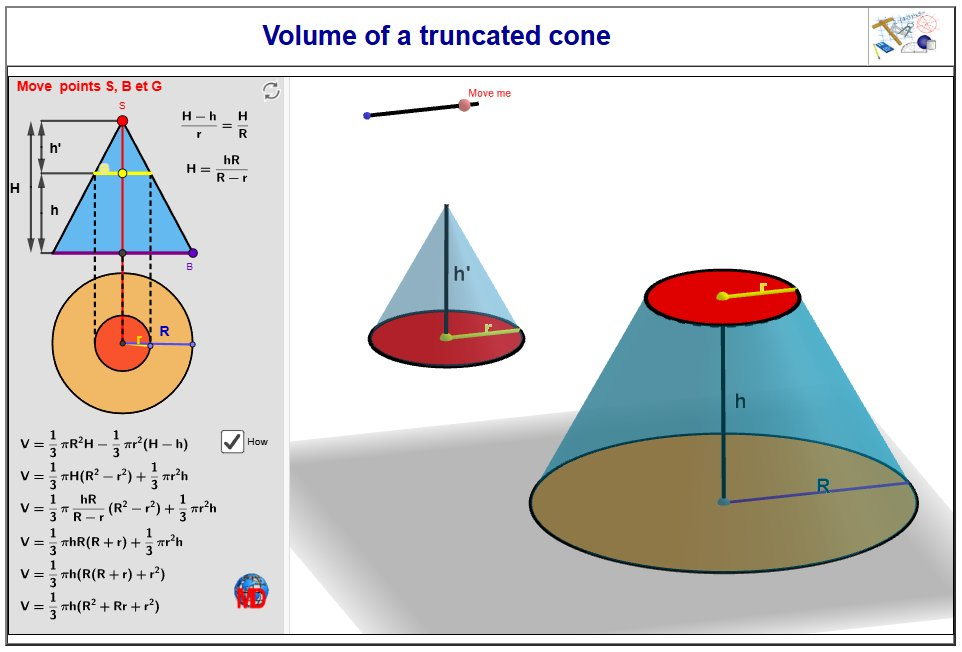
Ο Πάπυρος της Μόσχας και ο Όγκος της Κόλουρης Πυραμίδας

Ο Πάπυρος της Μόσχας περιλαμβάνει ένα ενδιαφέρον αριθμητικό παράδειγμα που αναφέρεται στον υπολογισμό του όγκου μιας κόλουρης πυραμίδας. 

Ακολουθώντας τα βήματα του παραδείγματος, μπορούμε να καταλήξουμε στον γενικό τύπο για τον όγκο μιας κόλουρης πυραμίδας: 

Πρόβλημα: 

Αν σου πουν: Μια κόλουρη πυραμίδα ύψους $6$, με βάση $4$ και κορυφή $2$. Να υψώσεις το $4$ στο τετράγωνο, αποτέλεσμα $16$.

Euler Brick και Τέλειο Euler Brick

 

Το Ανασκαμμένο Δωδεκάεδρο: Ένα Πολύεδρο από Άλλο Σύμπαν

Στη γεωμετρία, το ανασκαμμένο δωδεκάεδρο ξεχωρίζει ως ένα αστρικό πολύεδρο που αψηφά τις συμβατικές μορφές. 

Με μια πρώτη ματιά, μοιάζει με το κανονικό δωδεκάεδρο, όμως μια πιο προσεκτική παρατήρηση αποκαλύπτει τη μοναδικότητά του: οι $12$ πενταγωνικές του όψεις δεν είναι επίπεδες, αλλά «σκαμμένες» προς τα μέσα, σχηματίζοντας κοίλες πενταγωνικές πυραμίδες. Το αποτέλεσμα;

Γνωρίζετε ότι ...

Τον τύπο για τον όγκο της σφαίρας 

$V={\displaystyle \frac{4}{3}}\pi r^3$

τον βρήκε πρώτος ο Αρχιμήδης. Ο Αρχιμήδης (3ος αιώνας π.Χ.) χρησιμοποίησε μια πρωτοποριακή μέθοδο εξάντλησης, 

δηλαδή μια πρώιμη μορφή ολοκλήρωσης, για να υπολογίσει τον όγκο της σφαίρας συγκρίνοντάς τον με τον όγκο του κυλίνδρου που την περιβάλλει. Ανακάλυψε επίσης ότι η σφαίρα έχει τα ${\displaystyle \frac{2}{3}}$ του όγκου του κυλίνδρου που την περιέχει.

Volume of a truncated cone

Click here.

ο Γεωμετρικό Πρόβλημα του Κύβου και των Σφαιρών

Στο εσωτερικό ενός κύβου ακμής $1$ εγγράφουμε μια σφαίρα. Στη συνέχεια, εγγράφουμε $8$ μικρές σφαίρες στα κενά, όπως φαίνεται στην παρακάτω εικόνα.  

Βρείτε τον όγκο της περιοχής που περικλείεται από τον κύβο αλλά βρίσκεται εκτός των $9$ σφαιρών.

Λύνοντας τον Γρίφο του Πρίγκιπα Ρούπερτ με το GeoGebra – Ο Κώστας Δόρτσιος Εξηγεί

Εισαγωγικά

Ο κύβος του Rupert ή καλύτερα του Πρίγκιπα Rupert de Rhin (1619- 1682) είναι ένα πρόβλημα που επινοήθηκε από τον Άγγλο αυτόν πρίγκιπα του βασιλιά της Αγγλίας Κάρολου του δευτέρου και το οποίο έλυσε ο άγγλος John Wallis (1616 - 1703). 

Τη λύση του John Wallis την βελτίωσε ύστερα από εκατό χρόνια ο Ολλανδός Peter Nieuwland και επειδή δεν πρόλαβε να την ανακοινώσει τη λύση αυτή την δημοσίευσε ο Jean Henri von Swinden.

Διαβάστε περισσότερα εδώ και κάντε κλικ στην εικόνα για να δείτε το αρχείο Geogebra.

• Η σχετική ανάρτηση του Eisatopon εδώ.

Η Διαδρομή της Κάμπιας στο Οκτάεδρο

Κάθε έδρα του οκταέδρου $ABCDEF$ στην παρακάτω εικόνα είναι ένα ισόπλευρο τρίγωνο με πλευρά $a$. Μία κάμπια βρίσκεται αρχικά στο κέντρο της έδρας $ABC$ και θέλει να κινηθεί στο κέντρο της έδρας $CDF$.

Η κάμπια μπορεί να κινείται μόνο στην επιφάνεια του οκταέδρου. Ποια είναι η συντομότερη απόσταση που πρέπει να διανύσει η κάμπια για να φτάσει στον προορισμό της;

Ακεραίοι Διαγώνιοι σε Παραλληλεπίπεδα: Ένα Άλυτο Μαθηματικό Ζήτημα

Σίγουρα υπάρχουν ορθογώνια παραλληλεπίπεδα των οποίον οι ακμές και οι διαγώνιοι των εδρών τους είναι όλοι ακέραιοι αριθμοί. Για παράδειγμα, το $1719$, ο Paul Halcke ανακάλυψε ένα τέτοιο με διαστάσεις $(a,b,c)=(44,117,240)$ και διαγώνιες των εδρών $(d,e,f)=(125,244,267)$.

Το ερώτημα είναι αν υπάρχει ένα ορθογώνιο παραλληλεπίπεδο, στο οποίο και η εσωτερική του διαγώνιος (η οποία εμφανίζεται με κόκκινο) να έχει επίσης ακέραιο μήκος.

Το Φαινόμενο του Πρίγκιπα Rupert ή Ιδιότητα Rupert

Η Ερώτηση του Πρίγκιπα Ρούπερτ (17ος αιώνας):

Ο πρίγκιπας Ρούπερτ του Ρήνου (1619-1682) αναρωτήθηκε αν ένας κύβος μπορούσε να περάσει μέσα από μια τομή σε έναν άλλο κύβο ίδιου μεγέθους.

Η Απόδειξη του John Wallis:

Ο Άγγλος μαθηματικός John Wallis (1616-1703) απέδειξε ότι αυτό είναι πράγματι εφικτό. Ένας κύβος μπορεί να περιστραφεί κατάλληλα, ώστε μια διαγώνια τομή να δημιουργήσει ένα άνοιγμα αρκετά μεγάλο για να περάσει ένας άλλος κύβος ίδιου μεγέθους.

Ολικό εμβαδόν κυλίνδρου

Ολικό εμβαδόν επιφανείας κυλίνδου (παράπλευρη επιφάνεια + 2 βάσεις).

Αποδείξεις χωρίς λόγια.

Χιονάνθρωπος με διαβήτη

Ο Φαίδων θέλει να δημιουργήσει έναν χιονάνθρωπο από τρεις σφαίρες. Η χιονόμπαλα που έχει στη διάθεσή του είναι μια σφαίρα με ακτίνα $6$ ίντσες. 

Πρέπει να αποφασίσει ποιες θα είναι οι ακτίνες της βάσης, του κορμού και του κεφαλιού του χιονάνθρωπου με τους εξής περιορισμούς:

• Η ακτίνα του κορμού δεν πρέπει να είναι μεγαλύτερη από την ακτίνα της βάσης.
• Η ακτίνα του κεφαλιού δεν πρέπει να είναι μεγαλύτερη από την ακτίνα του κορμού.
• Όλες οι ακτίνες πρέπει να είναι θετικοί ακέραιοι αριθμοί.

Η ερώτηση είναι αν είναι δυνατόν να βρει ο Φαίδων ακτίνες για τις τρεις σφαίρες, έτσι ώστε να πληρούν τους παραπάνω περιορισμούς και να χρησιμοποιοήσει και τις $6$ ίντσες της χιονόμπαλας του.

Volume of Dodecahedron

Η δίεδρη γωνία μεταξύ δύο επιπέδων

Εμβαδόν επιφάνειας σφαίρας !

Κόκκινοι και πράσινοι κύβοι

Υπάρχουν τρεις κόκκινοι κύβοι ίσοι μεταξύ τους και τρεις πράσινοι κύβοι ίσοι μεταξύ τους και μικρότεροι από τους κόκκινους κύβους. 

Ο συνολικός όγκος των έξι κύβων είναι $840$ cm³. Εάν ένας πύργος κατασκευαστεί με τους έξι κύβους, το ύψος του πύργου είναι $30$ cm. Βρείτε τις διαστάσεις των κύβων γνωρίζοντας ότι τα μήκη των ακμών τους είναι ακέραιοι αριθμοί.

Οκτώ ράβδοι

Από 8 ίδιες ράβδους σχηματίστηκε ένα παραλληλεπίπεδο. Μία από τις διαστάσεις της κάθε ράβδου είναι 3.

Ποιος είναι ο όγκος κάθε ράβδου;

Περιοδικό Quantum

Όγκος στερεού εκ περιστροφής

Πρόβλημα

Ο κύβος με κορυφές $(0,0,0)$, $(1,0,0)$, $(0,1,0)$, $(1,1,0)$, $(0,0,1)$, $(1,0,1)$, $(0,1,1)$, $(1,1,1)$ περιστρέφεται γύρω από την ευθεία που διέρχεται από τα σημεία $(0,0,0)$ και $(1,1,1)$. Να υπολογιστεί ο όγκος του στερεού που δημιουργείται.

Η λύση του Κώστα Δόρτσιου:

Πράγματι το θέμα αυτό έχει την ομορφιά του! Η περιστροφή του κύβου! Μια περιστροφή γύρω από ένα σταθερό άξονα, τη διαγώνιο του. Και φανταστείτε να ζητούσαμε ο άξονας αυτός να εκτελεί και μια δική του κίνηση...(Αστρονομία)

Το αποτέλεσμα φαίνεται στο ακόλουθο σχήμα:

Αν προσέξουμε το σχήμα αυτό το οποίο αναρτώ και στη δυναμική του μορφή τότε θα διακρίνουμε ότι το σχήμα αυτό αποτελείται από:

Κυλινδρικός δακτύλιος

Ένας δακτύλιος κατασκευάζεται από μια συμπαγή σφαίρα ανοίγοντας μια κυλινδρική οπή μέσα από το κέντρο της σφαίρας. 

Ο άξονας του κυλίνδρου διέρχεται από το κέντρο της σφαίρας. Όταν το δαχτυλίδι βρίσκεται σε μια επίπεδη επιφάνεια, έχει ύψος ακριβώς $2$ cm. Να βρεθεί ο όγκος του στερεού υλικού του δακτυλίου σε κυβικά εκατοστά;

The Platonic Solids

An Exploration of the Five Regular 
Polyhedra and the Symmetries 
of Three-Dimensional Space Abstract 

The five Platonic solids (regular polyhedra) are the tetrahedron, cube, octahedron, icosahedron, and dodecahedron. 

The regular polyhedra are three dimensional shapes that maintain a certain level of equality; that is, congruent faces, equal length edges, and equal measure angles. In this paper we discuss some key ideas surrounding these shapes.