Click to Translate Whole Page to Read and Solve
Τρίτη 15 Απριλίου 2025
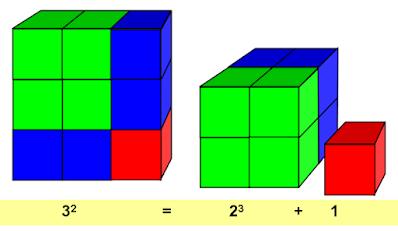
Αριθμός 19683
Σάββατο 12 Απριλίου 2025
cosx = x: Η Ομορφιά του Αριθμού Dottie

Κυριακή 6 Απριλίου 2025
Πέμπτη 3 Απριλίου 2025
Αριθμοί και Αγάπη - Η φανταστική ιστορία των φιλικών αριθμών
Ένα ταξίδι στην αρχαιότητα
Η ιστορία ξεκινά στην αρχαία Ελλάδα, όπου οι μαθηματικοί και οι φιλόσοφοι είχαν εμμονή με τις ιδιότητες των φυσικών αριθμών.
Τετάρτη 2 Απριλίου 2025
Taxicab Number 1729
και
Ονομάζεται «αριθμός ταξί» (taxicab number) από μια διάσημη ιστορία που αφορά τον μαθηματικό Ramanujan!
Διαβάστε την ιστορία εδώ.
Τρίτη 1 Απριλίου 2025
Ο Αριθμός 7: Όρια Αντίληψης, Συμβολισμός και Πολιτιστικές Επιρροές
Ο αριθμός 7 διαπερνά την ανθρώπινη ιστορία και κουλτούρα, συνδυάζοντας συμβολισμό, γνωστικά όρια και πολιτιστικές επιρροές. Είναι απλώς ένας αριθμός ή κάτι βαθύτερο;
🔹 Συμβολισμός και Πολιτιστικές Επιρροές
📜 Θρησκεία και Μυθολογία
-
Στη Βίβλο, το 7 συμβολίζει την πληρότητα και την τελειότητα: οι επτά ημέρες της δημιουργίας, οι επτά σφραγίδες της Αποκάλυψης.
Δευτέρα 31 Μαρτίου 2025
Μυστήριοι Διαδοχικοί Ακέραιοι
Πέμπτη 20 Μαρτίου 2025
Ο Μυστήριος Αριθμός 196: Lychrel ή Όχι;

Παρασκευή 7 Μαρτίου 2025
Ο Αριθμός 9 και οι Αγγελικές Τάξεις
Ο αριθμός 9 είναι ένας αριθμός με βαθιά συμβολική σημασία, ιδιαίτερα στη χριστιανική παράδοση. Στη θεολογία, συναντάμε την ταξινόμηση των αγγελικών υπάρξεων σε εννέα τάξεις, όπως περιγράφεται από τον Διονύσιο τον Αρεοπαγίτη.
Οι Εννέα Τάξεις των Αγγέλων
Σύμφωνα με τη χριστιανική παράδοση, οι άγγελοι είναι οργανωμένοι σε τρεις τριάδες, κάθε μία με ιδιαίτερο ρόλο και θέση στην ουράνια ιεραρχία:
Πρώτη Τριάδα (πλησιέστερη στον Θεό):
Σεραφείμ – Οι άγγελοι της αγάπης και της φωτιάς του Θεού.
Σάββατο 1 Μαρτίου 2025
Παρασκευή 28 Φεβρουαρίου 2025
Οι Κιστερκιανοί Αριθμοί: Ένα Αριθμητικό Σύστημα του Μεσαίωνα
Οι Κιστερκιανοί αριθμοί (Cistercian numerals) είναι ένα αριθμητικό σύστημα που αναπτύχθηκε από τους Κιστερκιανούς μοναχούς τον 13ο αιώνα. Αυτό το σύστημα επέτρεπε την αναπαράσταση οποιουδήποτε αριθμού από το 1 έως το 9.999 χρησιμοποιώντας έναν μόνο γλυφό (σύμβολο):
🔢 Πώς λειτουργεί το σύστημα;
- Βασίζεται σε έναν κάθετο άξονα, όπου τα ψηφία τοποθετούνται σε τέσσερις διαφορετικές περιοχές.
- Κάθε περιοχή του άξονα αντιπροσωπεύει μια τάξη μεγέθους:
Πέμπτη 27 Φεβρουαρίου 2025
Τετάρτη 26 Φεβρουαρίου 2025
Τρίτη 25 Φεβρουαρίου 2025
Αναζητώντας το Ένα: Άθροισμα Πρώτων Κλασμάτων
Παρασκευή 21 Φεβρουαρίου 2025
Έτη ως Γινόμενα Διαδοχικών Πρώτων Αριθμών
Τρίτη 18 Φεβρουαρίου 2025
Το Άθροισμα των Πρώτων 24 Τετραγώνων: Μια Μοναδική Μαθηματική Σύμπτωση

Δευτέρα 17 Φεβρουαρίου 2025
Επιστροφή Αριθμών: Κυκλική Σχέση Δυνάμεων και Αθροισμάτων
Κυριακή 16 Φεβρουαρίου 2025
Googol =
- Ετυμολογία: Η λέξη "googol" επινοήθηκε από τον Milton Sirotta, τον εννιάχρονο ανιψιό του μαθηματικού Edward Kasner, το
- Google: Η εταιρεία Google πήρε το όνομά της από το "googol", αντανακλώντας τη φιλοδοξία της να οργανώσει το τεράστιο όγκο πληροφοριών στο διαδίκτυο. Στην πραγματικότητα, το όνομα "Google" προήλθε από ένα τυπογραφικό λάθος της λέξης "googol". Ο Larry Page και ο Sergey Brin αποφάσισαν το όνομα googol, αλλά κατά την αναζήτηση διαθεσιμότητας, το όνομα καταχωρήθηκε λανθασμένα ως google.com, και τελικά το κράτησαν έτσι.
.png)




.jpg)
.gif)






.png)

.png)
