Ας εξετάσουμε τη σειρά των ακεραίων που αποτελούνται από όλους τους τέλειους τετράγωνους και κύβους, ξεκινώντας από το
Παρατηρούμε ότι το
Για χρόνια, μαθηματικοί και επιστήμονες υπολογιστών αναζητούσαν άλλα τέτοια παραδείγματα, αλλά, εκτός από το
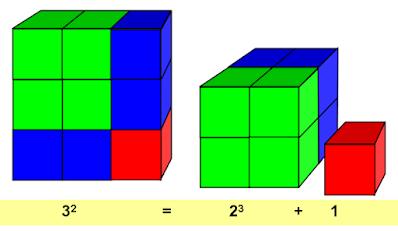




.jpg)



%20(1).png)

.png)








