Μυστήριοι Διαδοχικοί Ακέραιοι

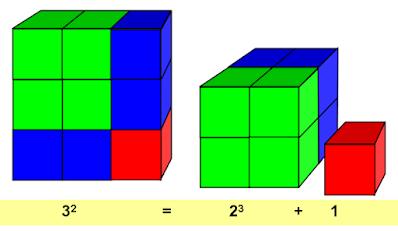
Ας εξετάσουμε τη σειρά των ακεραίων που αποτελούνται από όλους τους τέλειους τετράγωνους και κύβους, ξεκινώντας από το $4$: $$4,8,9,16,25,27,36,49,64,81,100,\dots$$

Παρατηρούμε ότι το $8$ και το $9$ είναι διαδοχικοί αριθμοί. Υπάρχουν άραγε άλλοι διαδοχικοί αριθμοί σε αυτήν τη σειρά;

Για χρόνια, μαθηματικοί και επιστήμονες υπολογιστών αναζητούσαν άλλα τέτοια παραδείγματα, αλλά, εκτός από το $8$ και το $9$, δεν βρέθηκαν ποτέ άλλες διαδοχικές δυνάμεις.

Αυτό το ερώτημα συνδέεται με την περίφημη Εικασία του Καταλάν, η οποία διατυπώθηκε από τον Βέλγο μαθηματικό Eugène Catalan το $1844$. Η εικασία υποστηρίζει ότι η μοναδική λύση στην εξίσωση:

$$x^p-y^q=1$$

για $x,y,p,q$ ακέραιους με $p,q>1$, είναι η περίπτωση $$3^2-2^3=9-8=1.$$

Η εικασία αυτή παρέμεινε άλυτη για περισσότερα από 150 χρόνια, έως ότου αποδείχθηκε τελικά από τον Ρουμάνο μαθηματικό Preda Mihăilescu, το 2002.