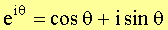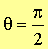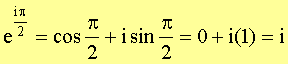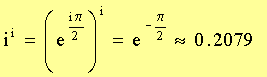Μην το κάνεις αυτό !

@AMRamosDelOlmo

Μέτρο 1

ΒΙΒΛΙΟ: Complex Numbers from A to ... Z (pdf)

Solving algebraic equations has been historically one of the favorite topics of mathematicians. While linear equations are always solvable in real numbers, not all quadratic equations have this property. The simplest such equation is $x^2+1=0$. 

 

Click on the image.

Until the 18th century, mathematicians avoided quadratic equations that were not solvable over R. Leonhard Euler broke the ice introducing the “number”  $\sqrt{-1}$  in his famous book Elements of Algebra as “ ... neither nothing, nor greater than nothing, nor less than nothing ... ” and observed “ ...

Στα αριστερά φανταστικοί αριθμοί στα δεξιά πραγματικοί !

@Cliff Pickover

Visualization of Euler's formula

A Brief History of the Complex Plane

ΒΙΒΛΙΟ (pdf): An Imaginary Tale: The Story of −1

Click on the image.

ln(−1)=π⋅i

Απόδειξη

Έχουμε διαδοχικά

$ln(-1)=\pi \cdot i$

$e^{ln(-1)}=e^{\pi i}$

$-1=e^{\pi i}$

$e^{\pi i}+1=0$

που είναι η ταυτότητα Euler.

Finding complex root of quadratic equation from graph

Από τις ρυθμίσεις επιλέξτε αυτόματη μετάφραση.

Trick to prove Euler's identity

Υπολογισμός λογαρίθμων μιγαδικών αριθμών

Computing logarithms of complex numbers

Η χρυσή τομή, το e, το i και ο αριθμός π

Από το 2023 στο 2025

Έστω $x,y\in (0,\pi /2)$ με 

$(\cos x+i\sin y{)}^{2023}=\cos (2023x)+i\sin (2023y)$ 

και 

$(\cos x+i\sin y{)}^{2024}=\cos (2024x)+i\sin (2024y)$.

Να αποδειχθεί ότι 

$$(\cos x+i\sin y{)}^{2025}=\cos (2025x)+i\sin (2025y).$$

De Moivre's Formula

Εξισώσεις τρίτου βαθμού: Το “χρέος” των μιγαδικών

Το αδιέξοδο, στο οποίο οδηγήθηκε η μέθοδος των “Καρντάνο – Ταρτάλια”, για το πρόβλημα της επίλυσης των τριτοβάθμιων εξισώσεων,

(1)

στην περίπτωση όπου,

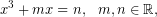
αποτέλεσε την αφορμή για την υλοποίηση της ιδέας της διεύρυνσης του συνόλου των πραγματικών στο σύνολο των μιγαδικών.

ii can be real!

Let us begin with the Euler’s Formula (please consult your complex number text book for further information):

Put

                                                

we get

Therefore,

Believe it or not…. “i to the power i” is only a small positive real number!

Φανταστικά υπόρριζα

Γινόμενο μιγαδικών αριθμών

Φανταστικά υπόρριζα

Να υπολογιστεί:

Euler’s Formula: A Complete Guide

In the world of complex numbers, as we integrate trigonometric expressions, we will likely encounter the so-called Euler’s formula.

Named after the legendary mathematician Leonhard Euler, this powerful equation deserves a closer examination — in order for us to use it to its full potential.

We will take a look at how Euler’s formula allows us to express complex numbers as exponentials, and explore the different ways it can be established with relative ease.

In addition, we will also consider its several applications such as the particular case of Euler’s identity, the exponential form of complex numbers, alternate definitions of key functions, and alternate proofs of de Moivre’s theorem and trigonometric additive identities.

Read more »