Το αδιέξοδο, στο οποίο οδηγήθηκε η μέθοδος των “Καρντάνο – Ταρτάλια”, για το πρόβλημα της επίλυσης των τριτοβάθμιων εξισώσεων,
(1) 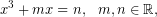
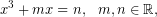
στην περίπτωση όπου,

αποτέλεσε την αφορμή για την υλοποίηση της ιδέας της διεύρυνσης του συνόλου 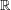 των πραγματικών στο σύνολο
των πραγματικών στο σύνολο  των μιγαδικών.
των μιγαδικών.
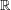 των πραγματικών στο σύνολο
των πραγματικών στο σύνολο  των μιγαδικών.
των μιγαδικών.Πλέον, με τη συγκρότηση του  , μπορεί να αναζητηθεί, για την (1), λύση της μορφής,
, μπορεί να αναζητηθεί, για την (1), λύση της μορφής,  , όπου,
, όπου, 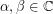 , τέτοια, ώστε,
, τέτοια, ώστε,
 , μπορεί να αναζητηθεί, για την (1), λύση της μορφής,
, μπορεί να αναζητηθεί, για την (1), λύση της μορφής,  , όπου,
, όπου, 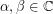 , τέτοια, ώστε,
, τέτοια, ώστε,
ή, ισοδύναμα, τέτοια ώστε,

Είναι αξιοσημείωτο ότι, στο πλαίσιο της αναζήτησης λύσης για το (Σ), ανακύπτουν βασικές έννοιες για το σύνολο  , όπως η έννοια του συζυγούς, του μέτρου και της τριγωνομετρικής μορφής ενός μιγαδικού αριθμού, καθώς και βασικά συμπεράσματα που τις διέπουν, με κυριότερο το Θεώρημα De Moivre.
, όπως η έννοια του συζυγούς, του μέτρου και της τριγωνομετρικής μορφής ενός μιγαδικού αριθμού, καθώς και βασικά συμπεράσματα που τις διέπουν, με κυριότερο το Θεώρημα De Moivre.
 , όπως η έννοια του συζυγούς, του μέτρου και της τριγωνομετρικής μορφής ενός μιγαδικού αριθμού, καθώς και βασικά συμπεράσματα που τις διέπουν, με κυριότερο το Θεώρημα De Moivre.
, όπως η έννοια του συζυγούς, του μέτρου και της τριγωνομετρικής μορφής ενός μιγαδικού αριθμού, καθώς και βασικά συμπεράσματα που τις διέπουν, με κυριότερο το Θεώρημα De Moivre.Παρατήρηση 1
Στο σύνολο  , μια εξίσωση της μορφής,
, μια εξίσωση της μορφής,  με
με 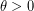 , ισοδύναμα, γράφεται,
, ισοδύναμα, γράφεται,
 , μια εξίσωση της μορφής,
, μια εξίσωση της μορφής,  με
με 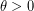 , ισοδύναμα, γράφεται,
, ισοδύναμα, γράφεται,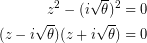
επομένως, έχει ακριβώς δύο λύσεις τις  και
και 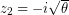 .
.
 και
και 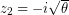 .
.Με βάση την προηγούμενη παρατήρηση, από τη δεύτερη εξίσωση του (Σ), έπεται ότι,
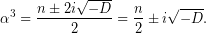
Οπότε, μια δυνατή επιλογή για το  , μπορεί να προκύψει από την ισότητα,
, μπορεί να προκύψει από την ισότητα,
 , μπορεί να προκύψει από την ισότητα,
, μπορεί να προκύψει από την ισότητα,(2) 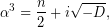
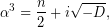
ενώ, η αντίστοιχη επιλογή για το 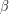 πρέπει να πληροί,
πρέπει να πληροί,
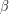 πρέπει να πληροί,
πρέπει να πληροί,(3) 

Αν υποτεθεί ότι υπάρχει, για τη (2), λύση της μορφής,
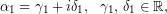
εύλογα, διερωτάται κανείς, αν, όπως στην περίπτωση όπου 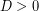 , ο αντίθετος του συζυγή του
, ο αντίθετος του συζυγή του  ,
,
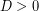 , ο αντίθετος του συζυγή του
, ο αντίθετος του συζυγή του  ,
,
είναι λύση της (3).
Η απάντηση είναι καταφατική και απορρέει από την ιδιότητα,
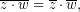
που, εύκολα, αποδεικνύεται ότι ισχύει για οποιουσδήποτε  .
.
 .
.Πράγματι,

Επειδή,

αρκεί, λόγω του (Σ), να βρεθούν 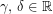 τέτοια, ώστε,
τέτοια, ώστε,
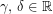 τέτοια, ώστε,
τέτοια, ώστε,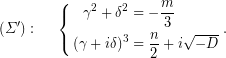
Παρατήρηση 2 Αφού  , προφανώς
, προφανώς 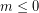 .
.
 , προφανώς
, προφανώς 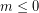 .
.Η πρώτη εξίσωση του (Σ΄), γράφεται,

Θέτουμε,
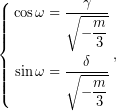
άρα,

(Με  συμβολίζονται το συνημίτονο και το ημίτονο αντίστοιχα.)
συμβολίζονται το συνημίτονο και το ημίτονο αντίστοιχα.)
 συμβολίζονται το συνημίτονο και το ημίτονο αντίστοιχα.)
συμβολίζονται το συνημίτονο και το ημίτονο αντίστοιχα.)Αντικαθιστώντας στη δεύτερη εξίσωση του (Σ΄),

επομένως,

Με τη βοήθεια γνωστών τριγωνομετρικών ταυτοτήτων,

Συνεπώς,
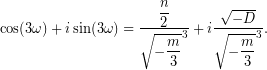
Άρα, αρκεί να βρεθεί γωνία  τέτοια, ώστε,
τέτοια, ώστε,
 τέτοια, ώστε,
τέτοια, ώστε,
Όμως,

δηλαδή, υπάρχουν άπειρες λύσεις για το παραπάνω σύστημα.
Αν 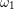 είναι μια τέτοια λύση, τότε,
είναι μια τέτοια λύση, τότε, 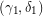 είναι λύση του (Σ΄), όπου,
είναι λύση του (Σ΄), όπου,
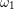 είναι μια τέτοια λύση, τότε,
είναι μια τέτοια λύση, τότε, 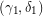 είναι λύση του (Σ΄), όπου,
είναι λύση του (Σ΄), όπου,
οπότε,  είναι λύση του (Σ), όπου,
είναι λύση του (Σ), όπου,
 είναι λύση του (Σ), όπου,
είναι λύση του (Σ), όπου,
Άρα,

είναι μία πραγματική λύση της (1).
Με τη βοήθεια αυτής της λύσης, η (1) μετασχηματίζεται ως εξής,


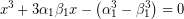

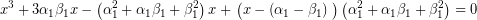
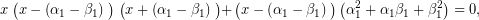
συνεπώς, γράφεται, τελικά,
(4) 

Το τριώνυμο,
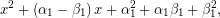
έχει διακρίνουσα,
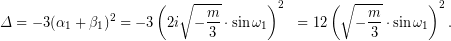
Τελικά, η (1), όταν  έχει τρεις πραγματικές λύσεις που δίνονται από τους τύπους,
έχει τρεις πραγματικές λύσεις που δίνονται από τους τύπους,
 έχει τρεις πραγματικές λύσεις που δίνονται από τους τύπους,
έχει τρεις πραγματικές λύσεις που δίνονται από τους τύπους,
Παράδειγμα 1 Για την εξίσωση,  , έχουμε,
, έχουμε,  , συνεπώς,
, συνεπώς,
 , έχουμε,
, έχουμε,  , συνεπώς,
, συνεπώς,
Αναζητείται  , τέτοιο, ώστε,
, τέτοιο, ώστε,
 , τέτοιο, ώστε,
, τέτοιο, ώστε,
οπότε, μπορεί να επιλεγεί ως 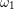 το
το 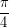 .
.
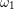 το
το 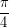 .
.Άρα, η εξίσωση έχει τρεις πραγματικές λύσεις,

Πηγή: dkonas

