Practice TEST 7
ΔΙΑΡΚΕΙΑ: 4 ΩΡΕΣ
ΘΕΜΑ 1ο
Κάθε διαγώνιος ενός κανονικού 2016-γωνου χρωματίζεται με ένα από  χρώματα έτσι ώστε αν δύο διαγώνιοι τέμνονται στο εσωτερικό του
χρώματα έτσι ώστε αν δύο διαγώνιοι τέμνονται στο εσωτερικό του  -γώνου, τότε έχουν διαφορετικό χρώμα. Ποια είναι η μικρότερη δυνατή τιμή του
-γώνου, τότε έχουν διαφορετικό χρώμα. Ποια είναι η μικρότερη δυνατή τιμή του 
 χρώματα έτσι ώστε αν δύο διαγώνιοι τέμνονται στο εσωτερικό του
χρώματα έτσι ώστε αν δύο διαγώνιοι τέμνονται στο εσωτερικό του  -γώνου, τότε έχουν διαφορετικό χρώμα. Ποια είναι η μικρότερη δυνατή τιμή του
-γώνου, τότε έχουν διαφορετικό χρώμα. Ποια είναι η μικρότερη δυνατή τιμή του 
ΘΕΜΑ 2ο
Το σημείο  βρίσκεται στο εσωτερικό του τριγώνου
βρίσκεται στο εσωτερικό του τριγώνου  ώστε
ώστε  . Το σημείο
. Το σημείο  είναι τέτοιο ώστε το
είναι τέτοιο ώστε το  είναι παραλληλόγραμμο. Να δειχθεί ότι
είναι παραλληλόγραμμο. Να δειχθεί ότι 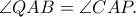
 βρίσκεται στο εσωτερικό του τριγώνου
βρίσκεται στο εσωτερικό του τριγώνου  ώστε
ώστε  . Το σημείο
. Το σημείο  είναι τέτοιο ώστε το
είναι τέτοιο ώστε το  είναι παραλληλόγραμμο. Να δειχθεί ότι
είναι παραλληλόγραμμο. Να δειχθεί ότι 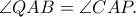
ΘΕΜΑ 3ο
Να βρεθούν όλοι οι θετικοί ακέραιοι  και
και  τέτοιοι ώστε ο
τέτοιοι ώστε ο  διαιρεί τον
διαιρεί τον  και ο
και ο  διαιρεί τον
διαιρεί τον 
 και
και  τέτοιοι ώστε ο
τέτοιοι ώστε ο  διαιρεί τον
διαιρεί τον  και ο
και ο  διαιρεί τον
διαιρεί τον 
ΘΕΜΑ 4ο
Η συνάρτηση  ορίζεται στους θετικούς ακέραιους ως εξής:
ορίζεται στους θετικούς ακέραιους ως εξής:
 ορίζεται στους θετικούς ακέραιους ως εξής:
ορίζεται στους θετικούς ακέραιους ως εξής:
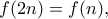 εάν ο
εάν ο  είναι άρτιος,
είναι άρτιος, εάν ο
εάν ο  είναι περιττός,
είναι περιττός, εάν ο
εάν ο  είναι άρτιος
είναι άρτιος εάν ο
εάν ο  είναι περιττός.
είναι περιττός.Να βρεθεί το πλήθος των θετικών ακεραίων  που είναι μικρότεροι ή ίσοι του
που είναι μικρότεροι ή ίσοι του  και έχουν την ιδιότητα
και έχουν την ιδιότητα 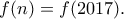
 που είναι μικρότεροι ή ίσοι του
που είναι μικρότεροι ή ίσοι του  και έχουν την ιδιότητα
και έχουν την ιδιότητα 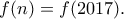
Πηγή: mathematica

