i. Αν  , να αποδείξετε ότι
, να αποδείξετε ότι
 , να αποδείξετε ότι
, να αποδείξετε ότι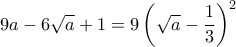 .
.
ii. Να βρείτε τους πραγματικούς αριθμούς  που ικανοποιούν την εξίσωση
που ικανοποιούν την εξίσωση
 που ικανοποιούν την εξίσωση
που ικανοποιούν την εξίσωση
Πρόβλημα 2
Πρόβλημα 3
Ένας γυμναστής γυμνάζει μιαν ομάδα αντρών. Αν τοποθετήσεις τους άντρες σε σειρές, ώστε να προκύπτει μια τετραγωνική διάταξη χρησιμοποιώντας τον μεγαλύτερο δυνατό αριθμό αντρών της ομάδας, τότε του περισσεύουν  άντρες. Αν θέλει να αυξήσει κατά έναν τους άντρες σε κάθε σειρά της πιο πάνω τετραγωνικής διάταξης, τότε του λείπουν
άντρες. Αν θέλει να αυξήσει κατά έναν τους άντρες σε κάθε σειρά της πιο πάνω τετραγωνικής διάταξης, τότε του λείπουν  άντρες.
άντρες.
 άντρες. Αν θέλει να αυξήσει κατά έναν τους άντρες σε κάθε σειρά της πιο πάνω τετραγωνικής διάταξης, τότε του λείπουν
άντρες. Αν θέλει να αυξήσει κατά έναν τους άντρες σε κάθε σειρά της πιο πάνω τετραγωνικής διάταξης, τότε του λείπουν  άντρες.
άντρες.
Να βρείτε τον αριθμό των αντρών της ομάδας που γυμνάζει ο γυμναστής συναρτήσει των  και
και  .
.
 και
και  .
.
Πρόβλημα 4
Δίνεται παραλληλόγραμμο  με
με  . Γράφουμε τους κύκλους διαμέτρων
. Γράφουμε τους κύκλους διαμέτρων  και
και  . Ονομάζουμε
. Ονομάζουμε  και
και 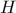 τα σημεία τομής των δύο κύκλων και
τα σημεία τομής των δύο κύκλων και  το μέσον του
το μέσον του  . Αν
. Αν  και
και  είναι τα συμμετρικά του
είναι τα συμμετρικά του  ως προς
ως προς  και
και 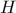 , αντίστοιχα, να αποδείξετε ότι τα σημεία
, αντίστοιχα, να αποδείξετε ότι τα σημεία  είναι κορυφές ρόμβου.
είναι κορυφές ρόμβου.
Πηγή
 με
με  . Γράφουμε τους κύκλους διαμέτρων
. Γράφουμε τους κύκλους διαμέτρων  και
και  . Ονομάζουμε
. Ονομάζουμε  και
και 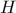 τα σημεία τομής των δύο κύκλων και
τα σημεία τομής των δύο κύκλων και  το μέσον του
το μέσον του  . Αν
. Αν  και
και  είναι τα συμμετρικά του
είναι τα συμμετρικά του  ως προς
ως προς  και
και 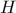 , αντίστοιχα, να αποδείξετε ότι τα σημεία
, αντίστοιχα, να αποδείξετε ότι τα σημεία  είναι κορυφές ρόμβου.
είναι κορυφές ρόμβου.Πηγή

 θετικών ακεραίων, για τα οποία ισχύει
θετικών ακεραίων, για τα οποία ισχύει  .
.