EisatoponAI: A simple way to show a formula in area

Area in parametric form

Let $C$ be a parametric curve given by :

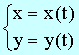
If the point $P(x,y)$, as t varies from $a$ to $b$, encircles a loop, the area is:

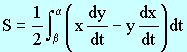
This formula is rather difficult to understand, here is a simple way to show the result.

Referring to the diagram, if T denotes the signed area of the triangle in yellow, then the increment of T,

dT = dS + dA

So that,

Since

After some short evaluation we have,

The result follows by taking integration.

An example

An ellipse is given by the curve :

The area enclosed by the ellipse is therefore :

Wow! We get our result easily.

Πηγή: qc.edu

EisatoponAI