The Nine Point Circle

In the early 19th century, Poncelet, Feuerbach and others showed that in any triangle, the following nine points are cyclic:the midpoint of each side of the triangle, the foot of each altitude, the midpoint of the interval joining each vertex of the triangle to the orthocentre.

That is, these nine points lie on a circle.

He also showed that the centre of this nine-point circle lies on the Euler line, and is the midpoint of the interval joining the circumcentre to the orthocentre.

Again, the proof is straightforward enough to present here as a structured exercise, although proving that the centre of the nine-point circle is the midpoint of OH is rather fiddly.

EXERCISE 27

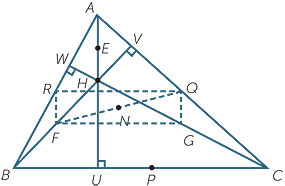The diagram to the right shows ABC with the altitudes AU, BV and CW meeting at the orthocenter H. The points E, F and G are the respective midpoints of AH, BH and CH. The points P, Q and R are the midpoints of the sides BC, CA and AB.

a

Prove that RQ and FG are each parallel
to BC and half its length.

b

Prove that RF and QG are each parallel to AH and half its length.

c

Hence prove that FGQR is a rectangle.

d

Prove similarly that FPQE is a rectangle.

e

Let N be the midpoint of FQ, and use the properties of a rectangle to prove that
RN = GN = FN = QN = PN = EN; and hence that R, G, F, Q, P and E are concyclic, lying on a circle with centre N .

f

By considering FQV, prove that N is equidistant from Q and V, and hence that the circle also passes through U, V and W.

g

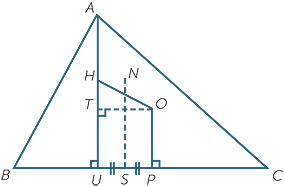The diagram to the right shows the altitude AU, the midpoint P of BC, the midpoint S of UP, and the circumcentre O, orthocentre H, and nine-point centre N.

i

Explain why SN is the perpendicular bisector of UP.

ii

Explain why SN, produced if necessary, bisects OH.

iii

Explain why N lies on OH, and is thus its midpoint.