Το θεώρημα του Bayes

Είναι ένας από τους πιο απλούς τύπους που θα μάθει ένας μαθηματικός. Κι όμως, οι συνέπειες του είναι αμέτρητες. Ικανές να σε κάνουν να απορείς πώς μπορεί κάτι τόσο απλό να ταρακουνήσει συθέμελα την επιστήμη.

Πρόκειται για μια από τις εξισώσεις που οι φοιτητές των θετικών επιστημών, αργά ή γρήγορα, θα συναντήσουν μπροστά τους. Μάλιστα, συνήθως αυτό γίνεται στα πρώτα χρόνια φοίτησης, καθώς το Θεώρημα του Bayes δεν είναι ούτε ακατανόητο, ούτε δύσμορφο όπως οι περισσότεροι τύποι. Με λίγη μαθηματική διαίσθηση, αυτό που διατύπωσε και απέδειξε ο Αγγλος μαθηματικός στις αρχές του 18ου αιώνα, γίνεται πλήρως αντιληπτό.

Τι εξηγεί αυτός ο απλούστατος νόμος; – Πώς να τον αποδείξετε, χρησιμοποιώντας ένα ζάρι

Το θεώρημα του Bayes ανήκει στην μεγάλη οικογένεια της «Θεωρίας των Πιθανοτήτων». Δεν είναι όμως ένα απλό μέλος της. Ο Harold Jeffreys, ένας από τους σπουδαιότερους Αγγλους μαθηματικούς, που ασχολήθηκε με τις «μπεϊζιανές» πιθανότητες και εισήγαγε την έννοια του αλγορίθμου Bayes, είχε δηλώσει πως ο συγκεκριμένος τύπος «είναι στη Θεωρία Πιθανοτήτων όπως αντίστοιχα το Πυθαγόρειο Θεώρημα στη Γεωμετρία».

Ο Bayes ασχολήθηκε με τις δεσμευμένες πιθανότητες ή αλλιώς τις «υπό συνθήκη» πιθανότητες. Ο νόμος του, μέσα στην συνοπτική του γραφή, κρύβει μυστικά που βασανίζουν από μαθηματικούς και φυσικούς, μέχρι γιατρούς και φιλοσόφους. Γράφοντας το «P(A|B) = P(B|A)*P(A)/ P(B)» ο Αγγλος μαθηματικός δεν περίμενε πως ο τύπος του, μετά από 300 χρόνια, θα έχει δημιουργήσει ολόκληρα φιλοσοφικά ερωτήματα. Πως θα έχει επηρεάσει την τεχνητή νοημοσύνη ή πως θα θέσει τις βάσεις για την εξέλιξη κλάδων όπως η κβαντομηχανική.

Τι σημαίνει όμως ο συγκεκριμένος τύπος; «Η πιθανότητα να συμβεί το ενδεχόμενο Α, δεδομένου του Β, ισούται με την πιθανότητα να συμβεί το Β δεδομένου του Α, επί την πιθανότητα να συμβεί το Α, διά την πιθανότητα να συμβεί το Β». Ο νόμος του Bayes γίνεται πολύ εύκολα αντιληπτός με ένα απλό παράδειγμα.

Εστω ότι ρίχνω ένα ζάρι και πληροφορούμαι ότι έφερα ζυγό αριθμό. Ποια η πιθανότητα να έχω φέρει $2$; Η απάντηση είναι $1/3$ και μπορεί να δοθεί άμεσα. Εχω φέρει ζυγό, άρα το αποτέλεσμα της ζαριάς είναι $2$ ή $4$ ή $6$. Κάθε ένα από αυτά έχει $1/3$ πιθανότητα να ισχύει.

Ας το δούμε τώρα μέσα από τον τύπο του Bayes: Η πιθανότητα να έχω φέρει ζυγό, αν ξέρω ότι έφερα $2$, είναι 100%. Η πιθανότητα να φέρω 2, χωρίς να ξέρω τίποτα, είναι $1/6$ (επειδή το ζάρι έχει $6$ πλευρές). Η πιθανότητα να φέρω ζυγό είναι 1/2. Βάζοντας τα νούμερα πάνω στην εξίσωση έχουμε ότι

$P(A|B) = (1* 1/6)/1/2 =1/3$.

Ενας... κρυμμένος θησαυρός – Οι συνέπειες του Bayes σε επιστήμη, τεχνητή νοημοσύνη αλλά και στον ανθρώπινο εγκέφαλο

Εχετε παρατηρήσει που μερικές φορές κάποια email μπαίνουν στον φάκελο με τα «ανεπιθύμητα» χωρίς να πρέπει; Αυτό συμβαίνει λόγω κάποιου σφάλματος στο αλγοριθμικό σύστημα, το οποίο βασίζεται στα λόγια του Bayes. Αναγνωρίζει κάποια στοιχεία του email (π.χ. συγκεκριμένες λέξεις, ή μαζικές αποστολές mail) και βάσει αυτών υπολογίζει την πιθανότητα το email να είναι ανεπιθύμητο. Αν η πιθανότητα είναι μεγάλη, τότε το μήνυμα πάει στα «junk». Με λίγα λόγια, υπολογίζει μια δεσμευμένη πιθανότητα.

Κάπως έτσι λειτουργεί και το «ψαχτήρι» της Google αλλά και οι σύγχρονες ρομποτικές μηχανές με εξελιγμένη τεχνητή νοημοσύνη. Ενα ακόμα πιο πρόσφατο παράδειγμα, είναι τα αυτοκινούμενα οχήματα. Για να αναγνωρίζουν την δομή του χώρου και να πάρουν αποφάσεις, ακολουθούν το «μπεϊζιανό» λογισμικό. Η ανεπτυγμένη ευφυΐα που παρουσιάζουν οι σημερινές μηχανές, οφείλεται εν πολλοίς σε αυτό το θεμελιώδες θεώρημα.

Οι συνέπειες του Bayes όμως δεν έχουν εφαρμογή μόνο στον χώρο της ρομποτικής. Οι φιλόσοφοι υποστηρίζουν πως ολόκληρη η επιστήμη μπορεί να θεωρηθεί ως μια «μπεϊζιανή» διαδικασία, όπως επίσης και ότι το θεώρημα του Bayes μπορεί να διακρίνει με τεράστια ακρίβεια την επιστήμη από την ψευδο-επιστήμη. Αν το σκεφτεί κανείς, η επιστήμη ξεκινάει από κάποια δεδομένα, γνωστά και ως αξιώματα. Δεχόμαστε ότι 1+0=1 και δεδομένου αυτού εξελίσουμε βήμα-βήμα την επιστήμη. Εχουμε κάνει όμως μια, έστω και υποτυπώδη, δέσμευση.

Οι επιστήμονες της γνωστικής επιστήμης, εικάζουν ότι το περιεχόμενο του θεωρήματος του Bayes είναι πιθανό να περνάει και εκτός των ορίων της επιστήμης. Μπορεί να βρίσκεται μέσα στον ίδιο μας τον... εγκέφαλο. Στον τρόπο με τον οποίο επεξεργαζόμαστε τα αμέτρητα δεδομένα, ώστε να καταλήξουμε σε κάποια απόφαση. Τον περασμένο Νοέμβριο, στην Νέα Υόρκη είχε λάβει μέρος ένα πολύ σημαντικό συνέδριο, γεμάτο με διακεκριμένους επιστήμονες και φιλοσόφους, με θέμα «Είναι ο εγκέφαλος Μπεϊζιανός;». Κάποια από τα γνωστότερα επιστημονικά περιοδικά έχουν επίσης ασχοληθεί με αυτό το εντυπωσιακό ερώτημα.

Το τεστ που εξαπατάει τους πάντες: Οταν ο νόμος του Bayes συγκρούεται με την... λογική

Πέραν όλων των άλλων, οι πιθανότητες του Bayes επηρεάζουν σημαντικά την ιατρική. Μάλιστα, σε αρκετές περιπτώσεις, τα αποτελέσματα που βγαίνουν μέσα από το θεώρημα του Αγγλου μαθηματικού δεν συμβαδίζουν με την κοινή λογική. Το παρακάτω παράδειγμα είναι χαρακτηριστικό.

Έστω ότι κάνατε ένα τεστ για μια ασθένεια Α που οι στατιστικές δείχνουν ότι προσβάλλεται 1 στους 100 ανθρώπους της ηλικίας σας. Αν το τεστ ήταν 100% αξιόπιστο, τότε δεν θα χρειαζόταν το θεώρημα του Bayes.

Όμως, τα ιατρικά τεστ διάγνωσης ποτέ δεν είναι 100% αξιόπιστα (τουλάχιστον μέχρι σήμερα). Ας πούμε λοιπόν πως το τεστ διάγνωσης της ασθένειας Α είναι 90% αξιόπιστο. Που σημαίνει ότι 90 στους 100 ανθρώπους που έχουν την ασθένεια Α βρίσκονται θετικοί στο τεστ, και 90 στους 100 ανθρώπους που δεν έχουν προσβληθεί από την εν λόγω ασθένεια βρίσκονται αρνητικοί στο τεστ.

Έστω ότι κάνετε το τεστ και βγήκε θετικό. Ποια είναι η πιθανότητα να έχετε προσβληθεί από την ασθένεια Α;

Ενώ η πρώτη απάντηση που έρχεται στο μυαλό των περισσότερων είναι 90% ή κάπου εκεί κοντά σ’ αυτό το νούμερο, η εφαρμογή του θεωρήματος Bayes δίνει ένα αναπάντεχο αποτέλεσμα: 8,33% !!

Ας δούμε γιατί, αφού πρώτα υιοθετήσουμε τον παρακάτω συμβολισμό:

$Ρ(Α) =$ η πιθανότητα ένα άτομο της ηλικίας σας να προσβληθεί από την ασθένεια $Α = 1/100 = 0,01$

$Ρ(Υ) =$ η πιθανότητα ένα άτομο της ηλικίας σας να μην έχει προσβληθεί από την ασθένεια $= 99/100 = 0,99$

$Ρ(Θ|Α) =$ η πιθανότητα το τεστ να είναι θετικό για ένα άτομο που φέρει την ασθένεια $= 90/100 = 0,9$

$Ρ(Θ|Υ) =$ η πιθανότητα το τεστ να είναι θετικό για ένα άτομο που είναι υγιές $= 10/100 = 0,1$

και $Ρ(Α|Θ) =$ το ζητούμενο, η πιθανότητα ένα άτομο που βρέθηκε θετικό στο τεστ να έχει προσβληθεί πράγματι από την ασθένεια $Α$.

Tότε, σύμφωνα με το θεώρημα του Bayes θα έχουμε:

Το αποτέλεσμα γίνεται πιο κατανοητό με το παρακάτω διάγραμμα:

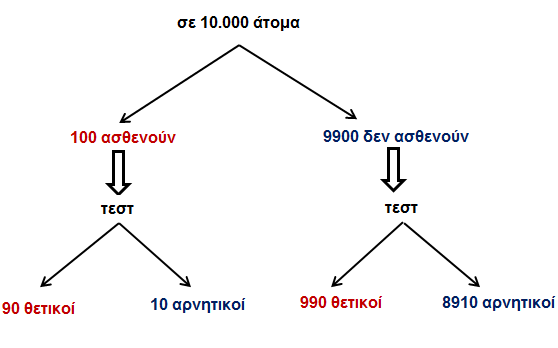
Βλέπουμε ότι σε σύνολο $90 + 990 = 1080$ ατόμων που βγήκαν θετικοί στο τεστ, μόνο οι $90$ πάσχουν από την ασθένεια οπότε: $Ρ(Α|Θ) = 90/1080 =0,083$.

Το ενδεχόμενο κατάχρησης του θεωρήματος αρχίζει από την εκ των προτέρων εκτίμηση της πιθανότητας $Ρ(A)$, που συχνά καλείται «prior». Στο παράδειγμα της ασθένειας Α θεωρήσαμε την τιμή $0,01$. Το ζήτημα είναι πως προκύπτει αυτή η εκτίμηση – ότι δηλαδή $1$ στους $100$ ανθρώπους μιας συγκεκριμένης ηλικίας προσβάλλονται από την συγκεκριμένη ασθένεια…. Σε πολλές περιπτώσεις η εκτίμηση της εκ των προτέρων πιθανότητας περιέχει υποκειμενικούς παράγοντες. Η εκτίμηση αυτής της πιθανότητας – όχι για την εκδήλωση μιας αρρώστιας – αλλά για κάτι που ίσως δεν υπάρχει όπως τα πολυσύμπαντα, την πληθωριστική διαδικασία του σύμπαντος ή τον Θεό και στη συνέχεια η εφαρμογή του θεωρήματος προωθεί την ψευδο-επιστήμη και την δεισιδαιμονία.

Στο θεώρημα του Bayes βρίσκεται ενσωματωμένο ένα ηθικό μήνυμα: αν δεν είστε σχολαστικός στην αναζήτηση εναλλακτικών ερμηνειών για τα δεδομένα σας, τότε τα δεδομένα σας θα επιβεβαιώσουν ακριβώς αυτό που ήδη πιστεύετε….

Πηγή: euclides-blog