Το σπιράλ (σπείρα) του Θεόδωρου

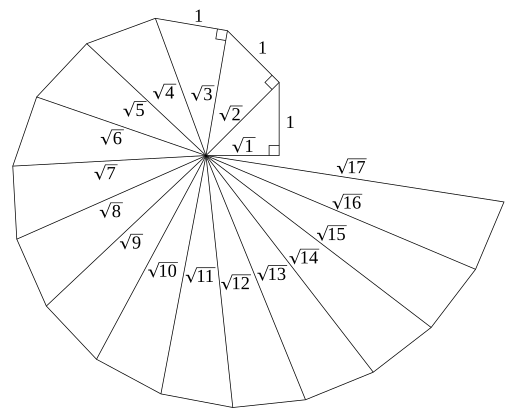
Η σπείρα αρχίζει με ένα ισοσκελές ορθογώνιο τρίγωνο, με κάθε σκέλος με μήκους την μονάδα . Ένα άλλο ορθογώνιο τρίγωνο σχηματίζεται, με το ένα σκέλος να είναι η υποτείνουσα του προηγούμενου τριγώνου (με μήκος $\sqrt{2}$) και το άλλο σκέλος που έχει μήκος $1$, το μήκος της υποτείνουσας αυτού του δεύτερου τριγώνου είναι $\sqrt{3}$. 

Σπείρα του Θεόδωρου με $16$ τρίγωνα

Στη συνέχεια η διαδικασία επαναλαμβάνεται. Το ν-ιοστό τρίγωνο στην αλληλουχία είναι ένα ορθογώνιο τρίγωνο με πλευρές $\sqrt{\nu }$ και $1$, και με υποτείνουσα $\sqrt{\nu }$ + $1$. Για παράδειγμα, το 16ο τρίγωνο έχει πλευρές μέτρησης $4$ (= $\sqrt{16}$), $1$ και υποτείνουσα του $\sqrt{17}$.

Σπείρα του Θεόδωρου με 110 τρίγωνα

Ο μικρότερος αριθμός τριγώνων που ολοκληρώνουν την στροφή της σπείρας βρίσκεται στην Εγκυκλοπαίδεια On-Line των Ακεραίων Ακολουθιών. Τα πρώτα μέλη είναι 17, 54, 110, 186,...

Πηγή: hellenicaworld

Σάρωση για να αποθηκεύσετε ή να κοινοποιήσετε την ανάρτηση