Πρόβλημα 1
Να προσδιορίσετε όλες τις συναρτήσεις 
τέτοιες, ώστε για κάθε 
να ισχύει ότι
τέτοιες, ώστε για κάθε να ισχύει ότι
.Βόρεια Μακεδονία
Πρόβλημα 2
Δίνεται τρίγωνο 
, του οποίου ο εγγεγραμμένος κύκλος εφάπτεται στις πλευρές 
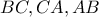στα σημεία 
αντίστοιχα. Δίνεται επιπλέον ότι υπάρχει σημείο 
στην ευθεία 
τέτοιο, ώστε 
. Έστω 
το μέσο του τόξου 
του περιγεγραμμένου κύκλου του τριγώνου το οποίο δεν περιέχει το σημείο 
. Να αποδείξετε ότι η ευθεία 
διέρχεται από το σημείο 
ή από το σημείο 
.
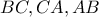, του οποίου ο εγγεγραμμένος κύκλος εφάπτεται στις πλευρές στα σημεία αντίστοιχα. Δίνεται επιπλέον ότι υπάρχει σημείο στην ευθεία τέτοιο, ώστε . Έστω το μέσο του τόξου του περιγεγραμμένου κύκλου του τριγώνου το οποίο δεν περιέχει το σημείο . Να αποδείξετε ότι η ευθεία διέρχεται από το σημείο ή από το σημείο .Ηνωμένο Βασίλειο
Πρόβλημα 3
Για κάθε θετικό ακέραιο 
, συμβολίζουμε με 
το πλήθος των διακεκριμένων πρώτων διαιρετών του (για παράδειγμα, 
και 
). Να προσδιορίσετε όλα τα πολυώνυμα 
με ακέραιους συντελεστές τέτοια, ώστε όταν ο είναι θετικός ακέραιος με 
, τότε ο 
είναι επίσης θετικός ακέραιος με 
.
, συμβολίζουμε με το πλήθος των διακεκριμένων πρώτων διαιρετών του (για παράδειγμα, και ). Να προσδιορίσετε όλα τα πολυώνυμα με ακέραιους συντελεστές τέτοια, ώστε όταν ο είναι θετικός ακέραιος με , τότε ο είναι επίσης θετικός ακέραιος με .Ελλάδα (Μίνος Μαργαρίτης - Ιάσονας Προδρομίδης)
Πρόβλημα 4
Να προσδιορίσετε τον μέγιστο ακέραιο 
για τον οποίο ισχύει το εξής: Οποτεδήποτε η Αλίκη χρωματίσει κόκκινους, 
ακριβώς αριθμούς από το σύνολο 
, ο Βασίλης μπορεί να χρωματίσει μπλε, κάποιους από τους υπόλοιπους αχρωμάτιστους αριθμούς έτσι, ώστε το άθροισμα όλων των κόκκινων αριθμών να είναι ίσο με το άθροισμα όλων των μπλε αριθμών.
για τον οποίο ισχύει το εξής: Οποτεδήποτε η Αλίκη χρωματίσει κόκκινους, ακριβώς αριθμούς από το σύνολο , ο Βασίλης μπορεί να χρωματίσει μπλε, κάποιους από τους υπόλοιπους αχρωμάτιστους αριθμούς έτσι, ώστε το άθροισμα όλων των κόκκινων αριθμών να είναι ίσο με το άθροισμα όλων των μπλε αριθμών.Πηγή: mathematica
