Έστω ισοσκελές ορθογώνιο τρίγωνο, $DAB (DA=DB)$. Με κέντρο σημείο $C$ της προς το $D$ προέκτασης του $BD$, γράφουμε κύκλο που διέρχεται από το $A$ και τέμνει το ευθύγραμμο τμήμα $AB$ στο $E$.
Έστω 
το σημείο τομής των 
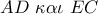. Υποθέτουμε ότι 
.
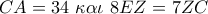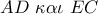το σημείο τομής των . Υποθέτουμε ότι 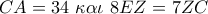.Βρείτε το εμβαδόν του 
.
.Πηγή: mathematica
Ομολογώ ότι δεν είναι για τρίτη Γυμνασίου, είναι κάπως δύσκολο για τα σχολικά δεδομένα, πιστεύω ότι θα ήταν καλό για τον Θαλή της τρίτης Γυμνασίου. Στο forum mathematica, το οποίο δεν γνωρίζω καθόλου( δεν το λέω για κακό, απλά το επισκέπτομαι για να δω την άσκηση όταν κάνει αναρτήσεις ο Σωκράτης), έχει δοθεί υποδειγματική λύση. Επομένως ,αν θέλετε, βρείτε κι άλλες.
ΑπάντησηΔιαγραφήΚαλησπέρα σας .
ΔιαγραφήΔεν έχετε άδικο η άσκηση είναι για διαγωνισμούς και το ήξερα .
Λόγοι που δεν είναι της παρούσης να αναλυθούν με υποχρέωσαν να την ανεβάσω για Γ γυμνασίου με 48 ώρες μόνο για μαθητές .
Ο κύριος που την έλυσε δεν σεβάστηκε το χρονικό περιορισμό ( έκανε όμως πράγματι υποδειγματική λύση )
Είχε τεθεί όμως η διευκρίνιση ότι ήταν αποδεκτές όλες οι λύσεις .
Έχει κι άλλες πράγματι λύσεις, εξ ίσου ωραίες, με ή χωρίς χρήση τριγωνομετρίας .
Ευχαριστώ
Νίκος Φραγκάκης .
Μια σχετικά απλή λύση χωρίς τριγωνομετρία
ΑπάντησηΔιαγραφήΑπό τα δεδομένα έχουμε:
EZ/ZC=7/8 => (EZ+ZC)/ZC=15/8 => 34/ZC=15/8 => ZC/34=8/15
Από την ομοιότητα των ορθογωνίων τριγώνων ADC, DCZ έχουμε:
ΖC/34=DC/AD => DC/AD=8/15 (1)
Τέλος από Π.Θ. (DC)^2+(AD)^2=34^2 (2)
Από τις (1) και (2) προκύπτει:
AD=30, DC=16
Επομένως: (ΑBC)= (30+16)*30/2 = 690
Καλησπέρα!!😀 Επί της ουσίας αυτή η λύση δεν διαφέρει από αυτήν που δόθηκε στο mathematica.gr. Θα ήθελα να δω και μία άλλη λύση, η οποία να διαφέρει αρκετά από τη δοθείσα.😉
ΔιαγραφήΜακάρι να έλθει τέτοια λύση και ακόμα πιο μακάρι να είναι από εσένα περιπατητικέ σχολιαστή!😄
ΔιαγραφήΚύριε Νίκο Φραγκάκη, αγαπητέ Doloros,
ΑπάντησηΔιαγραφήυποψιάζομαι πως η 'πρόκληση' του φίλου Μιχάλη δεν απευθύνεται μόνο σ' εμένα, αλλά και σ' εσάς. Φαντάζομαι ότι λύση που θα τον ικανοποιούσε θα ήταν μια που δεν θα έκανε χρήση της ομοιότητας των ορθογωνίων τριγώνων, αλλά αν κάνω λάθος ας με διορθώσει. Μια τέτοια λύση θα την ήθελα κι εγώ όπως έγραψα, αλλά δεν την ξέρω.
Παρακαλώ λοιπόν, όποτε κρίνετε εσείς καταλληλότερο, να την αναρτήσετε αν υπάρχει ή να σχολιάσετε σχετικά με το αν μπορεί να υπάρχει ή όχι..
Ευχαριστώ εκ των προτέρων
Θανάσης Παπαδημητρίου
Λιτές και πολύ κομψές ομολογουμένως και οι επόμενες λύσεις στο mathematica, ευχαριστώ πολύ τον κ. Φραγκάκη και τους φίλους τού forum!
ΑπάντησηΔιαγραφήΕυχαριστώ πολύ
Διαγραφή