ΑΣΚΗΣΗ 17
Δίνεται η συνάρτηση
, 
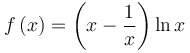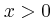.Δ1) Να αποδείξετε ότι ισχύει:
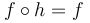όπου 
, 
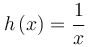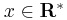.Δ2) Να αποδείξετε ότι η συνάρτηση f είναι γνησίως φθίνουσα στο διάστημα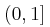 
και γνησίως αύξουσα στο διάστημα 
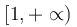και στη συνέχεια να βρείτε το σύνολο τιμών της.
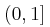και γνησίως αύξουσα στο διάστημα 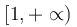και στη συνέχεια να βρείτε το σύνολο τιμών της.Δ3) Να αποδείξετε ότι η εξίσωση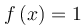 
έχει μία τουλάχιστον ρίζα στο διάστημα 
.
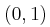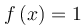έχει μία τουλάχιστον ρίζα στο διάστημα 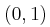.Δ4) Να αποδείξετε ότι η μοναδική ασύμπτωτη της γραφικής παράστασης της συνάρτησης f είναι η κατακόρυφη ευθεία με εξίσωση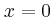 
.
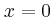.Δ5) Να αποδείξετε ότι η συνάρτηση f είναι κυρτή στο ανοικτό διάστημα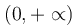 
.
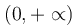.Δ6) Θεωρούμε παραγωγίσιμη συνάρτηση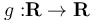 
με συνεχή παράγωγο 
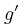για τις οποίες ισχύουν:
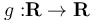με συνεχή παράγωγο 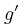για τις οποίες ισχύουν:
για κάθε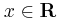 
Να αποδείξετε ότι για κάθε 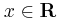ισχύει:
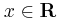ισχύει: 
