Η συνάρτηση Lambert W και το Θέμα Β των Μαθηματικών των Πανελληνίων εξετάσεων το 2021

ΘΕΜΑ Β 

Δίνεται η συνάρτηση $f: R \rightarrow R$ για την οποία ισχύει ότι 

$f(χ+1)=(χ+1)e^{-χ}$, $χ \in R$

για κάθε $χ \in R$.

Β1. Να δείξετε ότι 

$f(χ)=χe^{1-χ}$, $χ \in R$.

Β2. Να μελετήσετε τη συνάρτηση $f$ ως προς τη μονοτονία και τα ακρότατα.

Β3. Να μελετήσετε τη συνάρτηση $f$ ως προς την κυρτότητα, τα σημεία καμπής και να βρείτε τις ασύμπτωτες της γραφικής της παράστασης, αν υπάρχουν. 

Β4. Να βρείτε:

i) το σύνολο τιμών της συνάρτησης $f $

ii) το πλήθος των ριζών της εξίσωσης $f(χ)=λ$, για τις διάφορες τιμές του $λ \in R$.

Αυτό το θέμα δόθηκε στις Πανελλήνιες εξετάσεις το 2021, αν ενδιαφέρεστε για το σύνολο των θεμάτων θα τα βρείτε στο mathematica. 

Δείτε τις ενδεικτικές απαντήσεις τις Κεντρικής Επιτροπής Εξετάσεων εδώ.

Εμείς θα ασχοληθούμε με το δεύτερο θέμα.

Η συνάρτηση που κυριαρχεί στο θέμα αυτό είναι η 

$f(x)=xe^{1-x}$ 

της οποίας η γραφική παράσταση είναι κάπως έτσι:

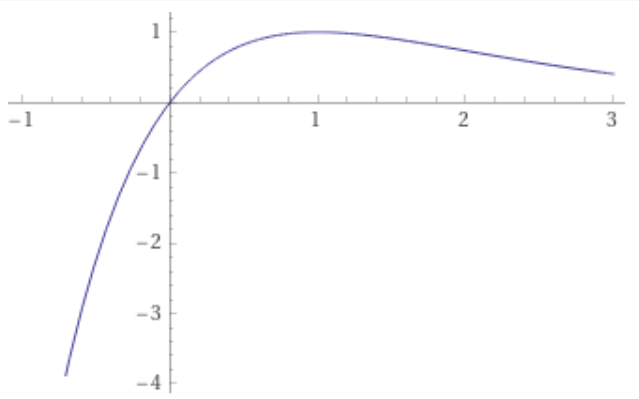
Θα αναζητήσουμε μια «κλειστή μορφή» των ριζών της εξίσωσης $f(x)=λ$, όπου $λ$ πραγματικός αριθμός. 

Έχουμε:

   

και θέτοντας , προκύπτει: 

. 

H εξίσωση αυτή μπορεί να λυθεί χρησιμοποιώντας την συνάρτηση Lambert W.

Η συνάρτηση Lambert, σύμφωνα με την θεωρία των μιγαδικών συναρτήσεων, είναι μια πλειότιμη συνάρτηση, δηλαδή οι κλάδοι της αντίστροφης συνάρτησης $f(w) = we^w$, όπου $w$ είναι οποιοσδήποτε μιγαδικός αριθμός. 

Για κάθε ακέραιο $k$ υπάρχει ένας κλάδος της πλειοτίμου συνάρτησης που συμβολίζεται με $W_k(z)$. Το $W_0$ ονομάζεται πρωτεύων κλάδος. 

Αυτές οι συναρτήσεις έχουν την εξής ιδιότητα: εάν τα $z$ και $w$ είναι μιγαδικοί αριθμοί, τότε η σχέση $we^w=z$ ισχύει, αν και μόνο αν $w=W_k(z)$, για κάποιον ακέραιο $k$.

Διαβάστε περισσότερα »