Εξίσωση με τέχνασμα

Να λυθεί στο σύνολο των πραγματικών αριθμών η εξίσωση:

$(x+1)(x+2)(x+3)(x+4)=99$

Λύση

Η άμεση κίνηση μας είναι να κάνουμε τις πράξεις και να καταλήξουμε στο πολυώνυμο:

$x^4+ 10x^3+ 35x^2+ 50 x – 75 = 0$

το οποίο διαπιστώνουμε ότι δεν έχει ρητές ρίζες.

Αν πάλι θεωρήσουμε την συνάρτηση

$φ( x ) = (x + 1) (x + 2) (x + 3) (x + 4)$

η οποία έχει ρίζες στο $x = − 1 , − 2 , − 3$, και $− 4$ και το γράφημα θα ήταν κάπως έτσι:

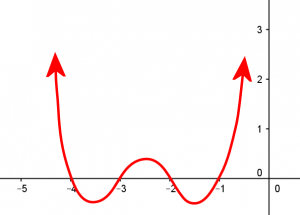
Οπότε οι λύσεις της εξίσωσης είναι τα σημεία όπου το γράφημα τέμνει την οριζόντια ευθεία $y= 99$. Kαι επειδή 

$φ(0) = 24$ και $φ(1) = 120$

οι λύσεις πρέπει να βρίσκονται μεταξύ των $x = 0$ και $x = 1$, που δεν υπάρχουν.

Μπορούμε να κάνουμε κάτι απλούστερο, να κάνουμε επιμεριστική ιδιότητα μεταξύ πρώτης - τέταρτης παρένθεσης και των άλλων δύο, οπότε έχουμε:

$(x^2+5x+4)(x^2+5x+6) = 99$

Παρατηρούμε ότι και οι δύο παρενθέσεις περιέχουν το $x^2 + 5x$, το οποίο μπορούμε να αντικαταστήσουμε με $t$, οπότε έχουμε διαδοχικά:

$(t + 4) (t + 6) = 99$

$t^2 + 10t – 75 = 0$

$(t + 15) (t – 5) = 0$

$t = -15$ ή $5$.

Αυτό συνεπάγεται ότι 

$x^2 + 5x = -15$ ή $x^2 + 5x = 5$;

οπότε 

$x = \dfrac{-5 \pm  i\sqrt{35} }{2}$  (αδύνατη στο $R$)

και 

$x = \dfrac{-5 \pm  \sqrt{45} }{2}$.