Δίνεται ένα τετράγωνο 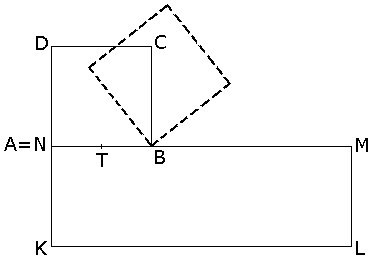$ABCD$ με πλευρά μήκους $a$ και ένα ορθογώνιο $KLMN$ με πλευρές μήκους $KL = 3a$ και $LM = α$. Στην αρχή, το τετράγωνο τοποθετείται έτσι ώστε το $A ≡ N$ και η πλευρά $AB$ να βρίσκονται στην πλευρά $NM$. 
Στρέφουμε το τετράγωνο $ABCD$ γύρω από το σημείο $Β$ έτσι ώστε η πλευρά $BC$ να βρίσκεται στην πλευρά $MN$. Περιστρέφοντας γύρω από τις κορυφές του (βλ. σχήμα), το τετράγωνο κινείται γύρω από την περίμετρο του ορθογωνίου $KLMN$ μέχρι να φτάσει ξανά στην αρχική του θέση.
α) Σχεδιάστε τη διαδρομή κατά μήκος της οποίας θα κινηθεί το σημείο $T$, που είναι το κέντρο της πλευράς $ΑΒ$.
β) Να βρεθεί το εμβαδόν της περιοχής που οριοθετείται από την καμπύλη που περιγράφεται από το σημείο $Τ$.
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου