A surprise in area and arc-length

Consider the first quadrant of a unit circle. Let s be any arc. Then the area between s and the x-axis plus the area between s and y-axis is a constant!

If we forget about the unit, then $A + B = s$

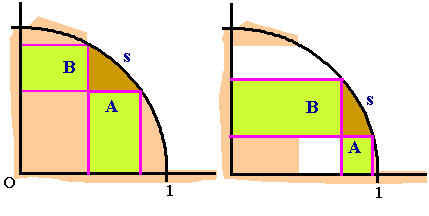
Note that the regions $A$ and $B$ overlap and that portion of area is counted twice. (in brown)

Let $P(x_1, y_1)$, $Q(x_2, y_2)$

The circle is $x^2 + y^2 = 1$

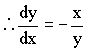
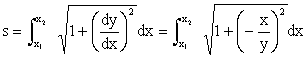
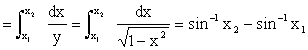
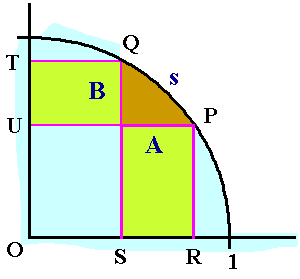
s = A + B

Sector Fun

Let $ÐPOR = a$, $ÐQOR = b$ in radians.

Then $s = b - a$.

$OP = OQ = 1$

A = sector POQ + DPOR - DQOS

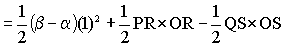
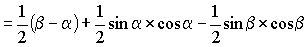
(equation 1)

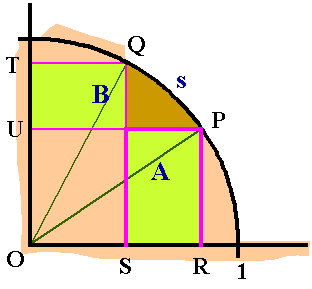
B = sector POQ + DQOT - DPOU

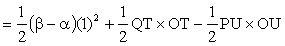
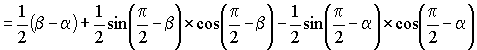
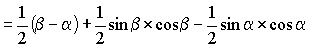(equation 2)

Adding equations 1 and 2, we get:

$A + B = a + b = s$.

Final Note :

Since the radius is 1, the two methods above are equivalent because:

.

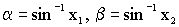Πηγή: qc.edu