Example of using Partial Fraction to evaluate Integral

Example of using Partial Fraction  to evaluate Integral
Problem   We like to evaluate the integral:                      where n = 1, 2, 3, 4.   We employ the technique of Partial Fractions. This algebraic  method is assumed to be known.
When n = 1,
When n = 2,          By using the substitution  x = tan q, it is a simple        exercise to get:                 Then,                 In getting (3) here, we change the variable  and apply (2). Alternatively, you can start by using the substitution   x = a tan q  at the beginning of (3).
When n = 3,
Finally you may check by changing the valuable suitably:
When n = 4,   Since  x4 + 1 cannot be factorized under rational numbers,  we start with the factorization :        x4 + 1 = (x4 + 2x2 + 1) – 2x2 =  (x2 + 1)2 – (Ö2 x)2 = (x2 + Ö2 x + 1)(x2 -Ö2 x +1)   As a Partial Fraction exercise, we get: 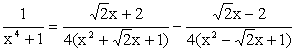 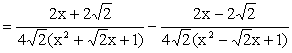 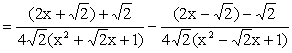 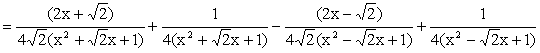 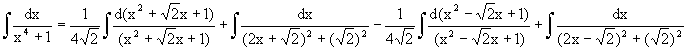 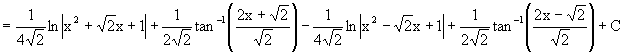                                                             Finally, if you still feel energetic of checking, we arrive: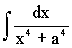

📘

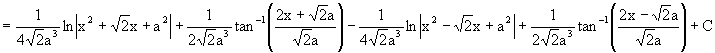
Έρχεται το πολλαπλό βιβλίο ΝΕΟ — βρες όλες τις επιλογές εδώ

PDF & Ψηφιακά Μαθησιακά Αντικείμενα — χωρίς εγγραφή • Portify

📚 437 βιβλία🎬 22.000+ Ψηφιακά Μαθησιακά Αντικείμενα

Δες τα βιβλία →