$A = I + \dfrac{Ε}{2} - 1$

Θεωρήστε ένα πολύγωνο $P$ σχεδιασμένο στο ευκλείδειο επίπεδο έτσι ώστε όλες οι κορυφές του $P$ να έχουν ακέραιες συντεταγμένες. Δηλαδή, αν σκεφτούμε το επίπεδο ως ένα γιγάντιο φύλλο χαρτιού, οι κορυφές του πολυγώνου βρίσκονται όλες στα δικτυωτά σημεία του χαρτιού. Το εμβαδόν του πολυγώνου μπορεί να υπολογιστεί μετρώντας τον αριθμό των σημείων πλέγματος μέσα στο πολύγωνο και τον αριθμό των σημείων πλέγματος στην άκρη του πολυγώνου. 

Αν 

$I$ = ο αριθμός των σημείων πλέγματος μέσα στο $P$

και

$E$ = ο αριθμός των σημείων πλέγματος κατά μήκος των άκρων του $P$, συμπεριλαμβανομένων των κορυφών, τότε το εμβαδόν $Α$ του $P$ δίνεται από τον τύπο: $A = I + \dfrac{Ε}{2} - 1$.

Για παράδειγμα, για το ακανόνιστο εξάγωνο παρακάτω, $I=13$ και $E=9$. Άρα ο τύπος μας προβλέπει ότι το εμβαδόν του πολυγώνου θα πρέπει να είναι:

$13 + 9/2 -1 = 16 1/2$.

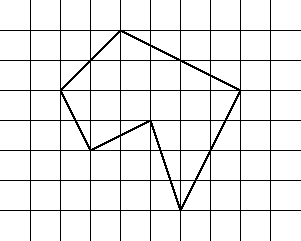
Μπορούμε να ελέγξουμε το αποτέλεσμά μας υπολογίζοντας το εμβαδόν του πολυγώνου. 

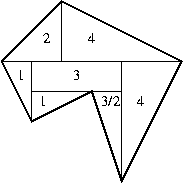
Χωρίζοντας το $P$ σε τρίγωνα και ορθογώνια, βλέπουμε ότι το εμβαδόν του είναι:

$2 + 4 + 1 + 3 + 4 + 1 + 3/2 = 16 1/2$.

ΠΡΟΒΛΗΜΑ:

• Να αποδείξετε ότι ο τύπος για το εμβαδόν του $P$ είναι σωστός για οποιοδήποτε τρίγωνο.
• Να αποδείξετε ότι ο τύπος για το εμβαδόν του $P$ είναι σωστός για οποιοδήποτε πολύγωνο, ανεξάρτητα από τον αριθμό των πλευρών.