Το 1966,ο Aυστριακός μαθηματικός Leo Moser έθεσε ένα ευφάνταστο όσο και πρακτικό ερώτημα: Έστω ένας διάδρομος με 1 μέτρο πλάτος, ποιο θα είναι το σχήμα και οι διαστάσεις του μεγαλυτέρου καναπέ που θα μπορούσε να "περάσει" από μια γωνία αυτού του διάδρομου; 
Ουσιαστικά το πρόβλημα προβάλλει στις δυο διαστάσεις ένα ζήτημα μεταφοράς επίπλου (καναπέ) του πραγματικού κόσμου. Το ερώτημα είναι να βρεθούν οι ακριβείς διαστάσεις του μεγαλύτερου επιπέδου σχήματος εμβαδού $Α$ ώστε να μπορεί να «περάσει» μέσα από ένα διάδρομο σχήματος $L$ με πλάτος $1$ μονάδα μήκους. Το εμβαδό $Α$ του μεγίστου σχήματος ονομάζεται σταθερά του καναπέ (sofa Constant).
Όλα αυτά πριν από $46$ χρόνια, όπου παραμένει ένα ανοικτό πρόβλημα.Το $1968$, ο Βρετανός John Michael Hammersley έδειξε ότι ένας καναπές σε σχήμα ακουστικού τηλεφώνου θα μπορούσε να «περάσει» την γωνία του διαδρόμου, ακόμη και αν το εμβαδό του είναι μεγαλύτερο από $2$ τετραγωνικά μέτρα (δείτε το σχήμα).
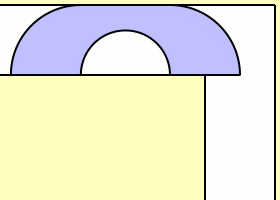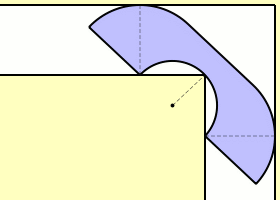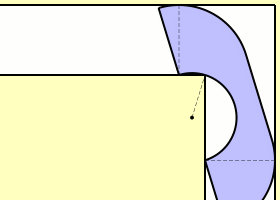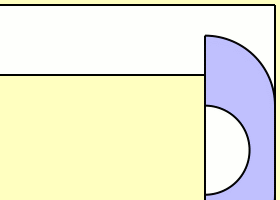
Η σταθερά του καναπέ (sofa Constant) σύμφωνα με τον Hammersley είναι μεγαλύτερη από $2.207416099$. Το $1992$, ο Joseph Gerver βελτίωσε την προσέγγιση του Hammersley, βρήκε ένα μεγαλύτερο κάτω άκρο της σταθεράς τον αριθμό $2.219531669$.
Το πρόβλημα όμως παραμένει ανοικτό.
Σχετικά προβλήματα 51-52 σελ 73-74 στη "χήρα με τα προβλήματα για την Γ Λυκείου" στο σύνδεσμο (drive.google.com/file)
Σχετικοί σύνδεσμοι:
Πηγή: mathhmagic
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου