Παρακάτω μπορείτε να βρείτε τα θέματα 23-30 των εισαγωγικών εξετάσεων της Κορέας για το 2024 στα μαθηματικά, για την ενότητα ανάλυση. Τα θέματα 23-28 είναι πολλαπλής επολογής και στα 29-30 ζητείτε μόνο η τελική απάντηση.
23. Ποιά είναι η τιμή του
 ; [2 μόρια]
; [2 μόρια]24. Για την παραμετρική καμπύλη  με παράμετρο
με παράμετρο  , ποιά η τιμή του
, ποιά η τιμή του  στο σημείο
στο σημείο  ; [3 μόρια]
; [3 μόρια]
 με παράμετρο
με παράμετρο  , ποιά η τιμή του
, ποιά η τιμή του  στο σημείο
στο σημείο  ; [3 μόρια]
; [3 μόρια]25. Δίνονται δυο συναρτήσεις  και
και  που ορίζονται και είναι παραγωγίσιμες στο σύνολο όλων των θετικών πραγματικών αριθμών. Η
που ορίζονται και είναι παραγωγίσιμες στο σύνολο όλων των θετικών πραγματικών αριθμών. Η  είναι η αντίστροφη συνάρτηση της
είναι η αντίστροφη συνάρτηση της  και η
και η  είναι συνεχής στο σύνολο των θετικών πραγματικών αριθμών. Αν για όλους τους θετικούς πραγματικούς αριθμούς
είναι συνεχής στο σύνολο των θετικών πραγματικών αριθμών. Αν για όλους τους θετικούς πραγματικούς αριθμούς  ισχύει
ισχύει
 και
και  που ορίζονται και είναι παραγωγίσιμες στο σύνολο όλων των θετικών πραγματικών αριθμών. Η
που ορίζονται και είναι παραγωγίσιμες στο σύνολο όλων των θετικών πραγματικών αριθμών. Η  είναι η αντίστροφη συνάρτηση της
είναι η αντίστροφη συνάρτηση της  και η
και η  είναι συνεχής στο σύνολο των θετικών πραγματικών αριθμών. Αν για όλους τους θετικούς πραγματικούς αριθμούς
είναι συνεχής στο σύνολο των θετικών πραγματικών αριθμών. Αν για όλους τους θετικούς πραγματικούς αριθμούς  ισχύει
ισχύει
26. Δίνεται ένα τρισδιάτατο σχήμα, όπως φαίνεται στην εικόνα, του οποίου η βάση περικλύεται από την καμπύλη  , τον άξονα
, τον άξονα  και τις δυο ευθείες
και τις δυο ευθείες  και
και  . Αν όλες οι τομές αυτού του σχήματος με επίπεδο κάθετο στον άξονα
. Αν όλες οι τομές αυτού του σχήματος με επίπεδο κάθετο στον άξονα  είναι τετράγωνα, ποιός είναι ο όγκος του; [3 μόρια]
είναι τετράγωνα, ποιός είναι ο όγκος του; [3 μόρια]
 , τον άξονα
, τον άξονα  και τις δυο ευθείες
και τις δυο ευθείες  και
και  . Αν όλες οι τομές αυτού του σχήματος με επίπεδο κάθετο στον άξονα
. Αν όλες οι τομές αυτού του σχήματος με επίπεδο κάθετο στον άξονα  είναι τετράγωνα, ποιός είναι ο όγκος του; [3 μόρια]
είναι τετράγωνα, ποιός είναι ο όγκος του; [3 μόρια]27. Έστω  η κλίση της ευθείας που διέρχεται από την αρχή των αξόνων και εφάπτεται της καμπύλης
η κλίση της ευθείας που διέρχεται από την αρχή των αξόνων και εφάπτεται της καμπύλης  , για
, για  πραγματικό αριθμό. Ποια η τιμής της
πραγματικό αριθμό. Ποια η τιμής της  για μια σταθερά
για μια σταθερά  , που ικανοποιεί την σχέση
, που ικανοποιεί την σχέση  ; [3 μόρια]
; [3 μόρια]
 η κλίση της ευθείας που διέρχεται από την αρχή των αξόνων και εφάπτεται της καμπύλης
η κλίση της ευθείας που διέρχεται από την αρχή των αξόνων και εφάπτεται της καμπύλης  , για
, για  πραγματικό αριθμό. Ποια η τιμής της
πραγματικό αριθμό. Ποια η τιμής της  για μια σταθερά
για μια σταθερά  , που ικανοποιεί την σχέση
, που ικανοποιεί την σχέση  ; [3 μόρια]
; [3 μόρια]28. Η συνάρτηση  είναι συνεχής στο σύνολο όλων των πραγματικών αριθμών και επίσης ισχύει
είναι συνεχής στο σύνολο όλων των πραγματικών αριθμών και επίσης ισχύει  , και για
, και για  είναι
είναι  . Για όλους τους θετικούς ακέραιους
. Για όλους τους θετικούς ακέραιους  , ο αριθμός των διαφορετικών ριζών της εξίσωσης
, ο αριθμός των διαφορετικών ριζών της εξίσωσης  , ως προς
, ως προς  , είναι
, είναι  . Έστω ότι η μικρότερη από τις δυο ρίζες είναι η
. Έστω ότι η μικρότερη από τις δυο ρίζες είναι η  και η μεγαλύτερη
και η μεγαλύτερη  . Οι δυο συναρτήσεις
. Οι δυο συναρτήσεις  ,
,  ικανοποιούν την σχέση
ικανοποιούν την σχέση  (όπου
(όπου  μια σταθερά) για όλους τους θετικούς ακέραιους.
μια σταθερά) για όλους τους θετικούς ακέραιους.
 είναι συνεχής στο σύνολο όλων των πραγματικών αριθμών και επίσης ισχύει
είναι συνεχής στο σύνολο όλων των πραγματικών αριθμών και επίσης ισχύει  , και για
, και για  είναι
είναι  . Για όλους τους θετικούς ακέραιους
. Για όλους τους θετικούς ακέραιους  , ο αριθμός των διαφορετικών ριζών της εξίσωσης
, ο αριθμός των διαφορετικών ριζών της εξίσωσης  , ως προς
, ως προς  , είναι
, είναι  . Έστω ότι η μικρότερη από τις δυο ρίζες είναι η
. Έστω ότι η μικρότερη από τις δυο ρίζες είναι η  και η μεγαλύτερη
και η μεγαλύτερη  . Οι δυο συναρτήσεις
. Οι δυο συναρτήσεις  ,
,  ικανοποιούν την σχέση
ικανοποιούν την σχέση  (όπου
(όπου  μια σταθερά) για όλους τους θετικούς ακέραιους.
μια σταθερά) για όλους τους θετικούς ακέραιους.Ποιά είναι η τιμή του

αν  ; [4 μόρια]
; [4 μόρια]
 ; [4 μόρια]
; [4 μόρια]29. Για τις δυο γεωμετρικές προόδους (ακολουθίες)  , των οποίων ο πρώτος όρος και ο λόγος είναι μη μηδενικοί, οι σειρές
, των οποίων ο πρώτος όρος και ο λόγος είναι μη μηδενικοί, οι σειρές  αντίστοιχα συγκλίνουν και ισχύει
αντίστοιχα συγκλίνουν και ισχύει
 , των οποίων ο πρώτος όρος και ο λόγος είναι μη μηδενικοί, οι σειρές
, των οποίων ο πρώτος όρος και ο λόγος είναι μη μηδενικοί, οι σειρές  αντίστοιχα συγκλίνουν και ισχύει
αντίστοιχα συγκλίνουν και ισχύει ,
, 
 .
.Αν

να βρείτε την τιμή του  . [4 μόρια]
. [4 μόρια]
 . [4 μόρια]
. [4 μόρια]30. Η παράγωγος 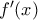 της παραγωγίσιμης σε όλο το σύνολο των πραγματικών αριθμών συνάρτησης
της παραγωγίσιμης σε όλο το σύνολο των πραγματικών αριθμών συνάρτησης  είναι
είναι  . Για θετικό αριθμό
. Για θετικό αριθμό  ας είναι
ας είναι 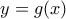 η εξίσωση της εφαπτόμενης από το σημείο
η εξίσωση της εφαπτόμενης από το σημείο  προς την καμπύλη
προς την καμπύλη  . Όταν απαριθμούμε κατά αύξουσα σειρά από τον μικρότερο προς τον μεγαλύτερο τους θετικούς ακέραιους
. Όταν απαριθμούμε κατά αύξουσα σειρά από τον μικρότερο προς τον μεγαλύτερο τους θετικούς ακέραιους  τέτοιους, ώστε η συνάρτηση
τέτοιους, ώστε η συνάρτηση 
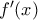 της παραγωγίσιμης σε όλο το σύνολο των πραγματικών αριθμών συνάρτησης
της παραγωγίσιμης σε όλο το σύνολο των πραγματικών αριθμών συνάρτησης  είναι
είναι  . Για θετικό αριθμό
. Για θετικό αριθμό  ας είναι
ας είναι 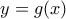 η εξίσωση της εφαπτόμενης από το σημείο
η εξίσωση της εφαπτόμενης από το σημείο  προς την καμπύλη
προς την καμπύλη  . Όταν απαριθμούμε κατά αύξουσα σειρά από τον μικρότερο προς τον μεγαλύτερο τους θετικούς ακέραιους
. Όταν απαριθμούμε κατά αύξουσα σειρά από τον μικρότερο προς τον μεγαλύτερο τους θετικούς ακέραιους  τέτοιους, ώστε η συνάρτηση
τέτοιους, ώστε η συνάρτηση 
να παρουσιάζει μέγιστο ή ελάχιστο (τοπικά) για  , ας είναι
, ας είναι  ο
ο  ιοστός. Να βρείτε την τιμή της παράστασης
ιοστός. Να βρείτε την τιμή της παράστασης  . [4 μόρια]
. [4 μόρια]
 , ας είναι
, ας είναι  ο
ο  ιοστός. Να βρείτε την τιμή της παράστασης
ιοστός. Να βρείτε την τιμή της παράστασης  . [4 μόρια]
. [4 μόρια]Πηγή: mathematica

 , ποια η τιμής της
, ποια η τιμής της  ; [3 μόρια]
; [3 μόρια]