ΘΕΜΑ 1ο
Αν  πραγματικοί αριθμοί τέτοιοι ώστε
πραγματικοί αριθμοί τέτοιοι ώστε  να δείξετε ότι η παράσταση
να δείξετε ότι η παράσταση
 πραγματικοί αριθμοί τέτοιοι ώστε
πραγματικοί αριθμοί τέτοιοι ώστε  να δείξετε ότι η παράσταση
να δείξετε ότι η παράσταση
όπου  και
και  είναι σταθερή, δηλαδή ανεξάρτητη των
είναι σταθερή, δηλαδή ανεξάρτητη των 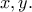
 και
και  είναι σταθερή, δηλαδή ανεξάρτητη των
είναι σταθερή, δηλαδή ανεξάρτητη των 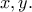
ΘΕΜΑ 2ο
Να βρείτε όλες τις τριάδες πρώτων αριθμών  για τις οποίες ισχύει
για τις οποίες ισχύει
 για τις οποίες ισχύει
για τις οποίες ισχύει
ΘΕΜΑ 3ο
Το τραπέζιο  έχει κάθετες διαγωνίους και έστω
έχει κάθετες διαγωνίους και έστω  τα μέσα των πλευρών
τα μέσα των πλευρών  αντίστοιχα. Στη βάση
αντίστοιχα. Στη βάση  θεωρούμε σημείο
θεωρούμε σημείο  τέτοιο ώστε
τέτοιο ώστε  Να βρείτε το μέτρο της γωνίας
Να βρείτε το μέτρο της γωνίας 
 έχει κάθετες διαγωνίους και έστω
έχει κάθετες διαγωνίους και έστω  τα μέσα των πλευρών
τα μέσα των πλευρών  αντίστοιχα. Στη βάση
αντίστοιχα. Στη βάση  θεωρούμε σημείο
θεωρούμε σημείο  τέτοιο ώστε
τέτοιο ώστε  Να βρείτε το μέτρο της γωνίας
Να βρείτε το μέτρο της γωνίας 
ΘΕΜΑ 4ο
Ένα σύνολο  αποτελούμενο από 4 στοιχεία θα λέγεται καλό αν για κάθε
αποτελούμενο από 4 στοιχεία θα λέγεται καλό αν για κάθε  ένας, τουλάχιστον, από τους αριθμούς
ένας, τουλάχιστον, από τους αριθμούς  και
και  ανήκει στο
ανήκει στο  Αν
Αν  το πλήθος όλων των καλών υποσυνόλων του συνόλου
το πλήθος όλων των καλών υποσυνόλων του συνόλου  να βρεθεί ο ελάχιστος θετικός ακέραιος
να βρεθεί ο ελάχιστος θετικός ακέραιος  τέτοιος ώστε
τέτοιος ώστε 
 αποτελούμενο από 4 στοιχεία θα λέγεται καλό αν για κάθε
αποτελούμενο από 4 στοιχεία θα λέγεται καλό αν για κάθε  ένας, τουλάχιστον, από τους αριθμούς
ένας, τουλάχιστον, από τους αριθμούς  και
και  ανήκει στο
ανήκει στο  Αν
Αν  το πλήθος όλων των καλών υποσυνόλων του συνόλου
το πλήθος όλων των καλών υποσυνόλων του συνόλου  να βρεθεί ο ελάχιστος θετικός ακέραιος
να βρεθεί ο ελάχιστος θετικός ακέραιος  τέτοιος ώστε
τέτοιος ώστε 
Επιμέλεια: Θανάσης Κοντογεώργης
Πηγή: mathematica
Σάρωση για να αποθηκεύσεις ή να κοινοποιήσεις την ανάρτηση

