Ramanujan’s Nested Radical Problem

In 1911, the Indian mathematical genius Srinivasa Ramanujan posed the above problem in the Journal of the Indian Mathematical Society. 

After waiting in vain for a few months, he himself provided a solution to the same! In this article, we go over Ramanujan’s solution (taking note of its spell-binding simplicity) along with exploring a calculus-based approach for the problem. So, let’s dive deep straight into it!

Disclaimer

But first, let us state us state a few important things explicitly.We will work on the assumption that the sequence given above converges. Strictly speaking, we should first prove the convergence of the sequence, and then go about finding its limit. However, for the sake of simplicity, we’d take the sequence’s convergence for granted, and just focus on finding the limit.

The solution presented below is not the exact one provided by Ramanujan in the journal. Rather, it’s a simplified version, the intention being to capture the gist of Ramanujan’s solution.

Ramanujan’s Solution

Okay, so let’s begin!

Note that for any non-negative real number x, we have —

Now, (x + 2) can again be written as ((x + 1) + 1), to get —

Carrying on with the process and writing (x + 3) as ((x + 2) + 1), we get —

The pattern is pretty visible by now. It’s clear that if we carry on this process infinitely, we’d land at —

Now comes the magic! Plugging in x = 2, we get —

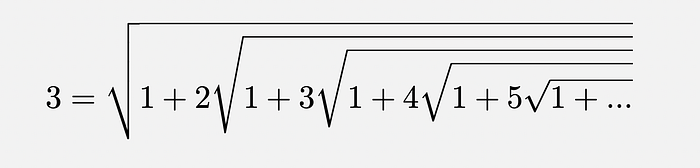
There we have it! The solution to our problem turns out to be just 3 !! Simple and plain as that. Indeed —

It’s hard not to wonder at the remarkable stroke of genius at the heart of this solution. Who would have thought that representing a number as the square root of its square could lead to such a beautiful identity?

Also, the above serves as an excellent example of a broader category of problems — wherein the problem posed is a particular case of more general identity. In such cases, we discover the general identity first and then plug in suitable values to get the desired result. For example, we can now easily say that —

So, that was Ramanujan’s solution to the problem. Next, we move on to explore a calculus-based approach for the same!

A Calculus-Based Solution

Another disclaimer: We assume the existence of a differentiable real-valued function f, defined implicitly as —

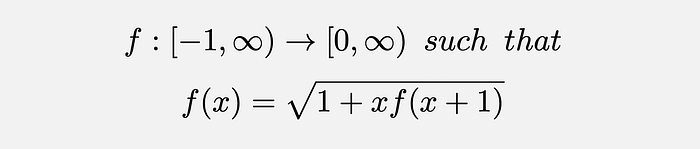
Again, we have forsaken some mathematical rigor here, by assuming that such a function exists without actually proving the same. Now, our goal is — provided such a function exists, can we exploit it to solve our original problem?

Note that —

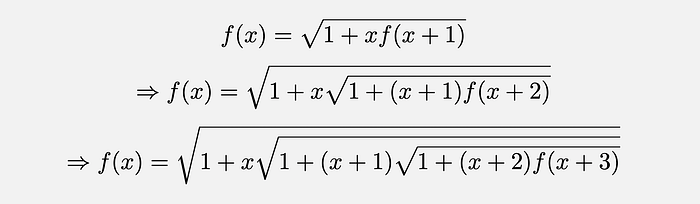
Carrying on, we arrive at —

As would be clearly visible by now, the solution to our problem is — f(2)! That is because,

Of course, the above is what inspired our function definition in the first place! Now, let’s try finding out the value of f(2).

Again,

Now, let’s see what the derivative of f(x) tells us!

Again, setting x = 0 in [3], we get —

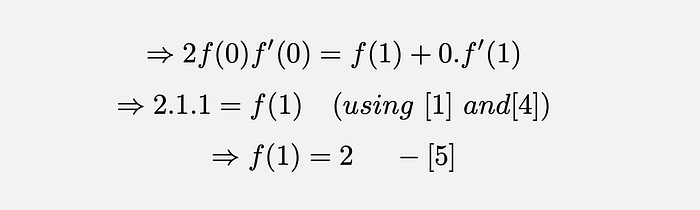
We’re almost there! Getting back to the original equation —

There we have it! The value of f(2), and thereby the answer to our problem, is 3!

Concluding Remarks

To add some historical context, Ramanujan published this problem in 1911, while trying to establish himself within the national mathematical community. A couple of years later, he’d get in contact with G.H. Hardy, move to Cambridge, and over the next five years the duo would go on to form one of the most productive mathematical partnerships ever.

Of course, Ramanujan is a name that needs no special introduction. His life and achievements have already been thoroughly documented. This article (as well as the problem posed by Ramanujan in the Journal of the Indian Mathematical Society) is merely a teaser from one of his favorite domains — nested radicals and continued fractions.

As was typical of him, Ramanujan possessed an all-absorbing interest in particular fields of mathematics, while remaining completely oblivious to the rest. Of course, who could have better understood this than Hardy himself! We end this article with a brilliant quote from him which aptly sums up Ramanujan—

The limitations of his knowledge were as startling as its profundity. Here was a man who could work out modular equations and theorems… to orders unheard of, whose mastery of continued fractions was… beyond that of any mathematician in the world; and yet he had never heard of a doubly periodic function or of Cauchy’s theorem, and had indeed but the vaguest idea of what a function of a complex variable was…

— G.H. Hardy

Πηγή: cantorsparadise