ΤΕΣΤ 1ο
ΘΕΜΑ 1
Έστω  το ακέραιο μέρος του
το ακέραιο μέρος του  και
και  το δεκαδικό του μέρος. Να λύσετε στο
το δεκαδικό του μέρος. Να λύσετε στο  την εξίσωση
την εξίσωση
 το ακέραιο μέρος του
το ακέραιο μέρος του  και
και  το δεκαδικό του μέρος. Να λύσετε στο
το δεκαδικό του μέρος. Να λύσετε στο  την εξίσωση
την εξίσωση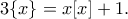
ΘΕΜΑ 2
Θεωρούμε οξυγώνιο τρίγωνο  το ύψος του
το ύψος του  και το ορθόκεντρό του
και το ορθόκεντρό του  Φέρουμε εφαπτομένη από το σημείο
Φέρουμε εφαπτομένη από το σημείο  στον κύκλο κέντρου
στον κύκλο κέντρου  και ακτίνας
και ακτίνας  και έστω
και έστω  το σημείο επαφής. Φέρουμε ακόμη εφαπτομένη από το
το σημείο επαφής. Φέρουμε ακόμη εφαπτομένη από το  στον κύκλο κέντρου
στον κύκλο κέντρου  και ακτίνας
και ακτίνας  και έστω
και έστω  το σημείο επαφής. Να δείξετε ότι η ευθεία
το σημείο επαφής. Να δείξετε ότι η ευθεία 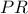 περνάει από δύο ίχνη υψών του τριγώνου
περνάει από δύο ίχνη υψών του τριγώνου 
 το ύψος του
το ύψος του  και το ορθόκεντρό του
και το ορθόκεντρό του  Φέρουμε εφαπτομένη από το σημείο
Φέρουμε εφαπτομένη από το σημείο  στον κύκλο κέντρου
στον κύκλο κέντρου  και ακτίνας
και ακτίνας  και έστω
και έστω  το σημείο επαφής. Φέρουμε ακόμη εφαπτομένη από το
το σημείο επαφής. Φέρουμε ακόμη εφαπτομένη από το  στον κύκλο κέντρου
στον κύκλο κέντρου  και ακτίνας
και ακτίνας  και έστω
και έστω  το σημείο επαφής. Να δείξετε ότι η ευθεία
το σημείο επαφής. Να δείξετε ότι η ευθεία 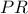 περνάει από δύο ίχνη υψών του τριγώνου
περνάει από δύο ίχνη υψών του τριγώνου 
ΘΕΜΑ 3
Οι θετικοί ακέραιοι  και
και  είναι τέτοιοι ώστε
είναι τέτοιοι ώστε
 και
και  είναι τέτοιοι ώστε
είναι τέτοιοι ώστε
Να δείξετε ότι ο  διαιρεί τον
διαιρεί τον  και ότι ο
και ότι ο  είναι της μορφής
είναι της μορφής  για κάποιον θετικό ακέραιο
για κάποιον θετικό ακέραιο 
 διαιρεί τον
διαιρεί τον  και ότι ο
και ότι ο  είναι της μορφής
είναι της μορφής  για κάποιον θετικό ακέραιο
για κάποιον θετικό ακέραιο 
ΘΕΜΑ 4
Σε μια ακολουθία θετικών ακεραίων, ονομάζουμε αντιστροφή ένας ζεύγος θέσεων για το οποίο ο όρος που βρίσκεται στα αριστερά είναι μεγαλύτερος από τον όρο στα δεξιά.
Για παράδειγμα, η ακολουθία 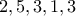 έχει ακριβώς πέντε αντιστροφές.
έχει ακριβώς πέντε αντιστροφές.
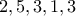 έχει ακριβώς πέντε αντιστροφές.
έχει ακριβώς πέντε αντιστροφές.Ποιος είναι ο μεγαλύτερος δυνατός αριθμός αντιστροφών που μπορεί να έχει μια ακολουθία θετικών ακεραίων με άθροισμα 

Επιμέλεια: Αθανάσιος Κοντογεώργης
Πηγή: mathematica

