Μαθηματικά κατεύθυνσης Γ΄ Λυκείου: Τράπεζα Θεμάτων - Θέμα 4ο (κωδ.23210)

Θεωρούμε συνάρτηση $f:\mathbb{R}\to \mathbb{R}$ δύο φορές παραγωγίσιμη στο $\mathbb{R}$ και στο παρακάτω σχήμα δίνεται η γραφική παράσταση της παραγώγου συνάρτησης $f^{\prime }(x)$.

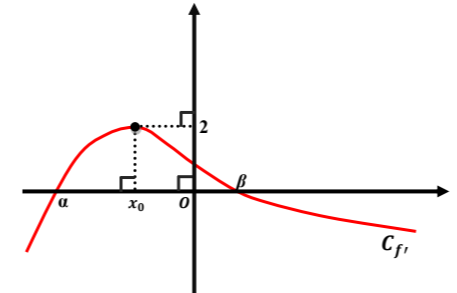
Γνωρίζουμε ότι:

• $\underset{x\to -\infty }{lim}f(x)=+\infty ,\underset{x\to +\infty }{lim}f(x)=-\infty$,
• τα $\alpha ,\beta$ είναι οι τετμημένες των μοναδικών δύο σημείων στα οποία τέμνει τον άξονα $x^{\prime }x$ η γραφική παράσταση της παραγώγου συνάρτησης $f^{\prime }(x)$
• $f(\alpha )<0,f(\beta )>0$
• η γραφική παράσταση της $f^{\prime }(x)$ παρουσιάζει ολικό ακρότατο στη θέση $x_0$

α) Να μελετηθεί ως προς τη μονοτονία και τα τοπικά ακρότατα η $f(x)$.

(Μονάδες 8)

β) Να αποδείξετε ότι η εξίσωση $f(x)=0$ έχει τρεις ακριβώς πραγματικές ρίζες.

(Μονάδες 9)

γ) Να αποδείξετε ότι για κάθε $x\in R$, ισχύει 

  $f(x+1)-f(x)\le 2$.

(Μονάδες 8)