Πρόβλημα 1ο
Έστω οξυγώνιο τρίγωνο  με
με  , το μέσο
, το μέσο  της πλευράς
της πλευράς  και ο περιγεγραμμένος κύκλος
και ο περιγεγραμμένος κύκλος  του τριγώνου
του τριγώνου  . Η εφαπτομένη του
. Η εφαπτομένη του  στο σημείο
στο σημείο  τέμνει την ευθεία
τέμνει την ευθεία  στο σημείο
στο σημείο  . Αν
. Αν  είναι το κέντρο του περιγεγραμμένου κύκλου του τριγώνου
είναι το κέντρο του περιγεγραμμένου κύκλου του τριγώνου 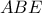 , να αποδείξετε ότι το μέσο του ευθύγραμμου τμήματος
, να αποδείξετε ότι το μέσο του ευθύγραμμου τμήματος  ανήκει στον
ανήκει στον  .
.
 με
με  , το μέσο
, το μέσο  της πλευράς
της πλευράς  και ο περιγεγραμμένος κύκλος
και ο περιγεγραμμένος κύκλος  του τριγώνου
του τριγώνου  . Η εφαπτομένη του
. Η εφαπτομένη του  στο σημείο
στο σημείο  τέμνει την ευθεία
τέμνει την ευθεία  στο σημείο
στο σημείο  . Αν
. Αν  είναι το κέντρο του περιγεγραμμένου κύκλου του τριγώνου
είναι το κέντρο του περιγεγραμμένου κύκλου του τριγώνου 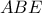 , να αποδείξετε ότι το μέσο του ευθύγραμμου τμήματος
, να αποδείξετε ότι το μέσο του ευθύγραμμου τμήματος  ανήκει στον
ανήκει στον  .
.(Ηνωμένο Βασίλειο)
Πρόβλημα 2ο
Συμβολίζουμε με  το σύνολο των θετικών ακεραίων. Να βρείτε όλες τις συναρτήσεις
το σύνολο των θετικών ακεραίων. Να βρείτε όλες τις συναρτήσεις  , τέτοιες ώστε για κάθε θετικό ακέραιο
, τέτοιες ώστε για κάθε θετικό ακέραιο  να ισχύουν τα πιο κάτω:
να ισχύουν τα πιο κάτω:
 το σύνολο των θετικών ακεραίων. Να βρείτε όλες τις συναρτήσεις
το σύνολο των θετικών ακεραίων. Να βρείτε όλες τις συναρτήσεις  , τέτοιες ώστε για κάθε θετικό ακέραιο
, τέτοιες ώστε για κάθε θετικό ακέραιο  να ισχύουν τα πιο κάτω:
να ισχύουν τα πιο κάτω:i) Το  είναι τέλειο τετράγωνο.
είναι τέλειο τετράγωνο.
 είναι τέλειο τετράγωνο.
είναι τέλειο τετράγωνο.(Αλβανία)
Πρόβλημα 3ο
Έστω θετικός ακέραιος  . Να βρείτε τον ελάχιστο θετικό ακέραιο
. Να βρείτε τον ελάχιστο θετικό ακέραιο  , για τον οποίο το πιο κάτω παιγνίδι μπορεί να συνεχιστεί επ' άπειρον:
, για τον οποίο το πιο κάτω παιγνίδι μπορεί να συνεχιστεί επ' άπειρον:
 . Να βρείτε τον ελάχιστο θετικό ακέραιο
. Να βρείτε τον ελάχιστο θετικό ακέραιο  , για τον οποίο το πιο κάτω παιγνίδι μπορεί να συνεχιστεί επ' άπειρον:
, για τον οποίο το πιο κάτω παιγνίδι μπορεί να συνεχιστεί επ' άπειρον:Θεωρούμε  κουτιά, τα
κουτιά, τα  . Για κάθε δείκτη
. Για κάθε δείκτη  , το κουτί
, το κουτί  περιέχει αρχικά ακριβώς
περιέχει αρχικά ακριβώς
 κουτιά, τα
κουτιά, τα  . Για κάθε δείκτη
. Για κάθε δείκτη  , το κουτί
, το κουτί  περιέχει αρχικά ακριβώς
περιέχει αρχικά ακριβώς νομίσματα. Σε κάθε βήμα του παιγνιδιού, εκτελούμε με τη σειρά τα πιο κάτω:
νομίσματα. Σε κάθε βήμα του παιγνιδιού, εκτελούμε με τη σειρά τα πιο κάτω:(1) Επιλέγουμε  κουτιά.
κουτιά.
 κουτιά.
κουτιά.(2) Από αυτά τα  κουτιά, επιλέγουμε
κουτιά, επιλέγουμε  και αφαιρούμε τουλάχιστον τα μισά νομίσματα από το καθένα. Δεδομένου ότι περίσσεψε το κουτί
και αφαιρούμε τουλάχιστον τα μισά νομίσματα από το καθένα. Δεδομένου ότι περίσσεψε το κουτί  , προσθέτουμε σε αυτό
, προσθέτουμε σε αυτό  νομίσματα.
νομίσματα.
 κουτιά, επιλέγουμε
κουτιά, επιλέγουμε  και αφαιρούμε τουλάχιστον τα μισά νομίσματα από το καθένα. Δεδομένου ότι περίσσεψε το κουτί
και αφαιρούμε τουλάχιστον τα μισά νομίσματα από το καθένα. Δεδομένου ότι περίσσεψε το κουτί  , προσθέτουμε σε αυτό
, προσθέτουμε σε αυτό  νομίσματα.
νομίσματα.(3) Αν κάποιο από τα κουτιά αδειάσει, το παιγνίδι τερματίζεται. Αλλιώς προχωρούμε στο επόμενο βήμα.
(Κύπρος)
Πρόβλημα 4ο
Θέτουμε  . Για κάθε θετικό ακέραιο
. Για κάθε θετικό ακέραιο  , ορίζουμε ως
, ορίζουμε ως  τον μικρότερο ακέραιο ο οποίος είναι μεγαλύτερος του
τον μικρότερο ακέραιο ο οποίος είναι μεγαλύτερος του  και έχει περισσότερους θετικούς διαιρέτες από τον
και έχει περισσότερους θετικούς διαιρέτες από τον  . Να αποδείξετε ότι το σύνολο
. Να αποδείξετε ότι το σύνολο
 . Για κάθε θετικό ακέραιο
. Για κάθε θετικό ακέραιο  , ορίζουμε ως
, ορίζουμε ως  τον μικρότερο ακέραιο ο οποίος είναι μεγαλύτερος του
τον μικρότερο ακέραιο ο οποίος είναι μεγαλύτερος του  και έχει περισσότερους θετικούς διαιρέτες από τον
και έχει περισσότερους θετικούς διαιρέτες από τον  . Να αποδείξετε ότι το σύνολο
. Να αποδείξετε ότι το σύνολο
είναι πεπερασμένο.
(Σκόπια)
Πηγή: mathematica

 διαιρεί το
διαιρεί το 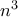 .
.