Πρόβλημα 1
Να βρείτε όλα τα ζεύγη  θετικών ακεραίων, για τα οποία ισχύει
θετικών ακεραίων, για τα οποία ισχύει  .
.
 θετικών ακεραίων, για τα οποία ισχύει
θετικών ακεραίων, για τα οποία ισχύει  .
.
Πρόβλημα 2
Έστω συνάρτηση  , για την οποία ισχύει
, για την οποία ισχύει  για κάθε
για κάθε  .
.
 , για την οποία ισχύει
, για την οποία ισχύει  για κάθε
για κάθε  .
.
Να αποδείξετε ότι:
i. Η  είναι
είναι  .
.
 είναι
είναι  .
.
ii.  , για κάθε
, για κάθε 
 , για κάθε
, για κάθε 
Πρόβλημα 3
Δίνεται παραλληλόγραμμο  με
με  . Γράφουμε τους κύκλους διαμέτρων
. Γράφουμε τους κύκλους διαμέτρων  και
και  . Ονομάζουμε
. Ονομάζουμε  και
και 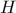 τα σημεία τομής των δύο κύκλων και
τα σημεία τομής των δύο κύκλων και  το μέσον του
το μέσον του  . Αν
. Αν  και
και  είναι τα συμμετρικά του
είναι τα συμμετρικά του  ως προς
ως προς  και
και 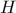 , αντίστοιχα, να αποδείξετε ότι τα σημεία
, αντίστοιχα, να αποδείξετε ότι τα σημεία  είναι κορυφές ρόμβου.
είναι κορυφές ρόμβου.
 με
με  . Γράφουμε τους κύκλους διαμέτρων
. Γράφουμε τους κύκλους διαμέτρων  και
και  . Ονομάζουμε
. Ονομάζουμε  και
και 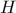 τα σημεία τομής των δύο κύκλων και
τα σημεία τομής των δύο κύκλων και  το μέσον του
το μέσον του  . Αν
. Αν  και
και  είναι τα συμμετρικά του
είναι τα συμμετρικά του  ως προς
ως προς  και
και 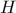 , αντίστοιχα, να αποδείξετε ότι τα σημεία
, αντίστοιχα, να αποδείξετε ότι τα σημεία  είναι κορυφές ρόμβου.
είναι κορυφές ρόμβου.
Πρόβλημα 4
Έστω 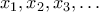 μια ακολουθία ακεραίων τέτοια, ώστε
μια ακολουθία ακεραίων τέτοια, ώστε  , για
, για 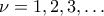
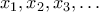 μια ακολουθία ακεραίων τέτοια, ώστε
μια ακολουθία ακεραίων τέτοια, ώστε  , για
, για 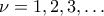
Να αποδείξετε ότι κάθε θετικός ακέραιος  είναι ίσος με μια διαφορά της μορφής
είναι ίσος με μια διαφορά της μορφής  για κάποια
για κάποια  και
και  .
.
 είναι ίσος με μια διαφορά της μορφής
είναι ίσος με μια διαφορά της μορφής  για κάποια
για κάποια  και
και  .
.