Πρόβλημα 1
Αν  είναι θετικοί πραγματικοί αριθμοί τέτοιοι ώστε
είναι θετικοί πραγματικοί αριθμοί τέτοιοι ώστε  , να αποδείξετε ότι:
, να αποδείξετε ότι:
 είναι θετικοί πραγματικοί αριθμοί τέτοιοι ώστε
είναι θετικοί πραγματικοί αριθμοί τέτοιοι ώστε  , να αποδείξετε ότι:
, να αποδείξετε ότι: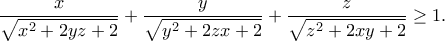
Να εξετάσετε πότε ισχύει η ισότητα.
Πρόβλημα 2
Θεωρούμε οξυγώνιο τρίγωνο  , με
, με  , εγγεγραμμένο σε κύκλο
, εγγεγραμμένο σε κύκλο  κέντρου
κέντρου  . Ονομάζουμε
. Ονομάζουμε  το βαρύκεντρο του τριγώνου
το βαρύκεντρο του τριγώνου και
και  τα ίχνη των υψών του από τις κορυφές
τα ίχνη των υψών του από τις κορυφές  , αντίστοιχα. Αν οι ημιευθείες
, αντίστοιχα. Αν οι ημιευθείες  τέμνουν τον
τέμνουν τον  στα
στα 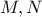 αντίστοιχα, να αποδείξετε ότι τα σημεία
αντίστοιχα, να αποδείξετε ότι τα σημεία  είναι ομοκυκλικά.
είναι ομοκυκλικά.
 , με
, με  , εγγεγραμμένο σε κύκλο
, εγγεγραμμένο σε κύκλο  κέντρου
κέντρου  . Ονομάζουμε
. Ονομάζουμε  το βαρύκεντρο του τριγώνου
το βαρύκεντρο του τριγώνου και
και  τα ίχνη των υψών του από τις κορυφές
τα ίχνη των υψών του από τις κορυφές  , αντίστοιχα. Αν οι ημιευθείες
, αντίστοιχα. Αν οι ημιευθείες  τέμνουν τον
τέμνουν τον  στα
στα 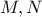 αντίστοιχα, να αποδείξετε ότι τα σημεία
αντίστοιχα, να αποδείξετε ότι τα σημεία  είναι ομοκυκλικά.
είναι ομοκυκλικά.
Πρόβλημα 3
Να βρεθούν όλες οι συναρτήσεις  , όπου
, όπου  είναι το σύνολο των θετικών ακέραιων, που είναι τέτοιες ώστε ο αριθμός
είναι το σύνολο των θετικών ακέραιων, που είναι τέτοιες ώστε ο αριθμός
 , όπου
, όπου  είναι το σύνολο των θετικών ακέραιων, που είναι τέτοιες ώστε ο αριθμός
είναι το σύνολο των θετικών ακέραιων, που είναι τέτοιες ώστε ο αριθμός 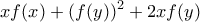
να είναι τέλειο τετράγωνο ακεραίου, για όλους τους θετικούς ακεραίους  .
.
 .
.
Πρόβλημα 4
Θεωρούμε έναν πρώτο αριθμό 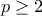 . O Άγγελος και ο Βαγγέλης παίζουν εναλλάξ το ακόλουθο παιχνίδι: Στον πίνακα υπάρχουν
. O Άγγελος και ο Βαγγέλης παίζουν εναλλάξ το ακόλουθο παιχνίδι: Στον πίνακα υπάρχουν άδεια κουτάκια στη σειρά, το ένα δίπλα στο άλλο, και σε κάθε κίνηση, ο παίκτης που έχει σειρά, βάζει σε ένα από τα κενά κουτάκια ένα μονοψήφιο μη αρνητικό ακέραιο.
άδεια κουτάκια στη σειρά, το ένα δίπλα στο άλλο, και σε κάθε κίνηση, ο παίκτης που έχει σειρά, βάζει σε ένα από τα κενά κουτάκια ένα μονοψήφιο μη αρνητικό ακέραιο.
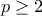 . O Άγγελος και ο Βαγγέλης παίζουν εναλλάξ το ακόλουθο παιχνίδι: Στον πίνακα υπάρχουν
. O Άγγελος και ο Βαγγέλης παίζουν εναλλάξ το ακόλουθο παιχνίδι: Στον πίνακα υπάρχουν άδεια κουτάκια στη σειρά, το ένα δίπλα στο άλλο, και σε κάθε κίνηση, ο παίκτης που έχει σειρά, βάζει σε ένα από τα κενά κουτάκια ένα μονοψήφιο μη αρνητικό ακέραιο.
άδεια κουτάκια στη σειρά, το ένα δίπλα στο άλλο, και σε κάθε κίνηση, ο παίκτης που έχει σειρά, βάζει σε ένα από τα κενά κουτάκια ένα μονοψήφιο μη αρνητικό ακέραιο.
Ο Άγγελος παίζει πρώτος και το παιχνίδι τελειώνει όταν γεμίσουν όλα τα κουτάκια και έτσι προκύπτει ένας  ψήφιος αριθμός
ψήφιος αριθμός  (ο οποίος επιτρέπουμε να έχει και μηδενικά στην αρχή).
(ο οποίος επιτρέπουμε να έχει και μηδενικά στην αρχή).
 ψήφιος αριθμός
ψήφιος αριθμός  (ο οποίος επιτρέπουμε να έχει και μηδενικά στην αρχή).
(ο οποίος επιτρέπουμε να έχει και μηδενικά στην αρχή).
Σκοπός του Άγγελου είναι ο αριθμός  να διαιρείται με το
να διαιρείται με το , ενώ σκοπός του Βαγγέλη είναι να το αποτρέψει. Να αποδείξετε ότι ο Άγγελος έχει στρατηγική νίκης.
, ενώ σκοπός του Βαγγέλη είναι να το αποτρέψει. Να αποδείξετε ότι ο Άγγελος έχει στρατηγική νίκης.
 να διαιρείται με το
να διαιρείται με το , ενώ σκοπός του Βαγγέλη είναι να το αποτρέψει. Να αποδείξετε ότι ο Άγγελος έχει στρατηγική νίκης.
, ενώ σκοπός του Βαγγέλη είναι να το αποτρέψει. Να αποδείξετε ότι ο Άγγελος έχει στρατηγική νίκης.