Θεώρημα της Πεταλούδας
Δίνεται εγγεγραμμένο σε κύκλο  (κέντρου
(κέντρου  ) τετράπλευρο
) τετράπλευρο  και ας είναι
και ας είναι  .
.
 (κέντρου
(κέντρου  ) τετράπλευρο
) τετράπλευρο  και ας είναι
και ας είναι  .
.Αν  είναι τα σημεία τομής της στο
είναι τα σημεία τομής της στο  καθέτου στην
καθέτου στην  με τις
με τις  αντίστοιχα , να δειχθεί ότι
αντίστοιχα , να δειχθεί ότι  το μέσο της
το μέσο της  .
.
 είναι τα σημεία τομής της στο
είναι τα σημεία τομής της στο  καθέτου στην
καθέτου στην  με τις
με τις  αντίστοιχα , να δειχθεί ότι
αντίστοιχα , να δειχθεί ότι  το μέσο της
το μέσο της  .
.θα ισχύει:
 .
. Όμως  είναι ομόλογα τμήματα των προφανώς ομοίων τριγώνων
είναι ομόλογα τμήματα των προφανώς ομοίων τριγώνων  (
( και
και 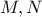 τα ίχνη των υψών και τα μέσα των ομολόγων πλευρών) και συνεπώς ο λόγος τουs θα ισούται με το λόγο των ομολόγων υψών τους δηλαδή
τα ίχνη των υψών και τα μέσα των ομολόγων πλευρών) και συνεπώς ο λόγος τουs θα ισούται με το λόγο των ομολόγων υψών τους δηλαδή
 είναι ομόλογα τμήματα των προφανώς ομοίων τριγώνων
είναι ομόλογα τμήματα των προφανώς ομοίων τριγώνων  (
( και
και 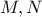 τα ίχνη των υψών και τα μέσα των ομολόγων πλευρών) και συνεπώς ο λόγος τουs θα ισούται με το λόγο των ομολόγων υψών τους δηλαδή
τα ίχνη των υψών και τα μέσα των ομολόγων πλευρών) και συνεπώς ο λόγος τουs θα ισούται με το λόγο των ομολόγων υψών τους δηλαδή .
. Από

το μέσο της  και το Θεώρημα της πεταλούδας έχει αποδειχθεί.
και το Θεώρημα της πεταλούδας έχει αποδειχθεί.
 και το Θεώρημα της πεταλούδας έχει αποδειχθεί.
και το Θεώρημα της πεταλούδας έχει αποδειχθεί.Πηγή: mathematica

 στις
στις  . Με
. Με  σύμφωνα με το
σύμφωνα με το 