Τα θέματα του διαγωνισμού SEEMOUS 2015

1) Να αποδειχθεί ότι για κάθε $x\in (0,1)$ ισχύει η ανισότητα:

 ${\displaystyle {\int }_0^1\sqrt{1+{\cos }^{2}y}dy>\sqrt{x^2+{\sin }^{2}x}}$. 

2) Για κάθε θετικό ακέραιο n, θεωρούμε τις συναρτήσεις $f_n:\mathbb{R}\to \mathbb{R}$, που ορίζονται από την αναδρομική σχέση $f_{n+1}(x)=f_1(f_n(x))$, όπου $f_1(x)=3x-4x^3$. 

Να λυθεί η εξίσωση $f_n(x)=0$. 

3) Για κάθε ακέραιο $n>2$, έστω $A,B,C,D\in {\mathcal{M}}_n(\mathbb{R})$ πίνακες για τους οποίους ισχύει $AC-BD=I_n$ και $AD+BC=O_n$. 

Να αποδειχθεί ότι: 

α) $CA-DB=I_n$ και $DA+CB=O_n$, 

β) $det(AC)\ge 0$ και $(-1{)}^{n}det(BD)\ge 0$. 

4) Έστω ένα ανοικτό σύνολο που περιέχει το και μια συνάρτηση κλάσης τέτοια, ώστε:

.

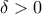α) Να αποδειχθεί ότι υπάρχει τέτοιο ώστε:
, για κάθε .
β) Για το του ερωτήματος α), ορίζουμε αναδρομικά την ακολουθία με: 

 

και

 

για κάθε .
Να μελετηθεί η σύγκλιση της σειράς

  , για .

Πηγή

Δείτε εδώ τα θέματα και λύσεις παρελθόντων ετών.