Σε οξυγώνιο τρίγωνο  φέρουμε τα ύψη
φέρουμε τα ύψη  και
και  . Έστω
. Έστω  το κέντρο του περιγεγραμμένου κύκλου του τριγώνου
το κέντρο του περιγεγραμμένου κύκλου του τριγώνου  . Να αποδείξετε, ότι η απόσταση του σημείου
. Να αποδείξετε, ότι η απόσταση του σημείου  από την ευθεία
από την ευθεία  είναι ίση με την απόσταση του σημείου
είναι ίση με την απόσταση του σημείου 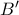 από την ευθεία
από την ευθεία  .
.
 φέρουμε τα ύψη
φέρουμε τα ύψη  και
και  . Έστω
. Έστω  το κέντρο του περιγεγραμμένου κύκλου του τριγώνου
το κέντρο του περιγεγραμμένου κύκλου του τριγώνου  . Να αποδείξετε, ότι η απόσταση του σημείου
. Να αποδείξετε, ότι η απόσταση του σημείου  από την ευθεία
από την ευθεία  είναι ίση με την απόσταση του σημείου
είναι ίση με την απόσταση του σημείου 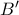 από την ευθεία
από την ευθεία  .
.
Λύση
Αρκεί να δείξουμε ότι $(AOB')
= (BOA')$ αφού έχουν βάσεις $OA\,\,\kappa \alpha \iota \,\,OB$ ίσες. Είναι:
$2(AOB') = AO \cdot AB' \cdot \sin \theta = R \cdot AB' \cdot \dfrac{{BA'}}{c}$
και
$2(BOA') = AO \cdot BA' \cdot \sin \omega = AO \cdot BA' \cdot \cos A$,
ή
$2(BOA') = AO \cdot BA' \cdot \sin \omega = AO \cdot BA' \cdot \cos A$,
ή
$2(BOA') = AO \cdot BA'
\cdot \dfrac{{AB'}}{c}$.
Άρα $(AOB') = (BOA')$
Άρα $(AOB') = (BOA')$





































Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου