Τρία ισοδύναμα θεωρήματα

ΘΕΩΡΗΜΑ ΤΟΥ ROLLE

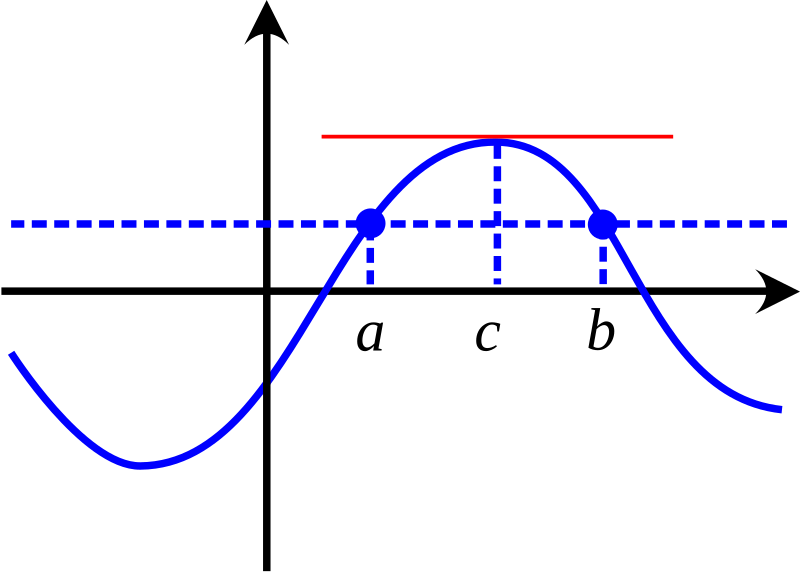
Έστω ότι η $y = f(x)$ είναι συνεχής στο διάστημα $[a, b]$ και ότι έχει παράγωγο στο διάστημα $(a, b)$. Αν $f(a) = f(b)$, τότε υπάρχει κάποιος $ξ$ στο $(a, b)$ ώστε 

$f'(ξ) = 0$.

ΘΕΩΡΗΜΑ ΜΕΣΗΣ ΤΙΜΗΣ ΤΟΥ ΔΙΑΦΟΡΙΚΟΥ ΛΟΓΙΣΜΟΥ (LAGRANGE)

Έστω ότι η $y = f(x)$ είναι συνεχής στο διάστημα $[a, b]$ και ότι έχει παράγωγο στο διάστημα $(a, b)$. Τότε υπάρχει κάποιος $ξ$ στο $(a, b)$ ώστε 

$\dfrac{f(b)−f(a)}{b−a} = f'(ξ)$.

ΘΕΩΡΗΜΑ ΜΕΣΗΣ ΤΙΜΗΣ ΤΟΥ ΔΙΑΦΟΡΙΚΟΥ ΛΟΓΙΣΜΟΥ (CAUCHY)

Έστω ότι οι $y = f(x)$ και $y = g(x)$ είναι συνεχείς στο διάστημα $[a, b]$ και παραγωγίσιμες στο $(a, b)$ έτσι ώστε $g(a)\neq{g(b)}$ και ώστε σε κανένα $x$ του $(a, b)$ να μην ισχύει $f' (x) = g' (x) = 0$. 

Τότε υπάρχει κάποιος $ξ$ στο $(a, b)$ ώστε 

$\dfrac{f(b)−f(a)}{g(b)−g(a)} = \dfrac{f'(ξ)}{g'(ξ)}$.

Το Θεώρημα Μέσης Τιμής (Cauchy) αποδεικνύεται βάσει του Θεωρήματος του Rolle, αλλά και το Θεώρημα Μέσης Τιμής (Lagrange) είναι ειδική περίπτωση του Θεωρήματος Μέσης Τιμής (Cauchy). 

Πράγματι, αν θεωρήσουμε την y = g(x) = x στο Θεώρημα Μέσης Τιμής (Cauchy), τότε προκύπτει το Θεώρημα Μέσης Τιμής (Lagrange). 

Τα τρία αυτά θεωρήματα είναι ισοδύναμα.